Hãy tìm số trung bình và mốt của các số liệu sau đây (kết quả làm tròn đến hàng phần trăm)
A, 12;32;93;78;24;12;54;66;78
B, 23;41;71;29;48;45;72;41
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
27 tháng 11 2023
a)
+ Làm tròn các số 52 và 27 đến hàng chục ta được các số 50 và 30.
Vậy tổng 52 + 27 có kết quả ước lượng là: 50 + 30 = 80.
+ Làm tròn các số 86 và 98 đến hàng chục ta được các số 90 và 100.
Vậy tổng 86 + 98 có kết quả ước lượng là: 90 + 100 = 190.
+ Làm tròn các số 73 và 56 đến hàng chục ta được các số 70 và 60.
Vậy tổng 73 + 56 có kết quả ước lượng là: 70 + 60 = 130.
b)
+ Làm tròn các số 472 và 326 đến hàng trăm ta được các số 500 và 300.
Vậy tổng 472 + 326 có kết quả ước lượng là: 500 + 300 = 800.
+ Làm tròn các số 623 và 401 đến hàng trăm ta được các số 600 và 400.
Vậy tổng 623 + 401 có kết quả ước lượng là: 600 + 400 = 1 000.
+ Làm tròn các số 359 và 703 đến hàng trăm ta được các số 400 và 700.
Vậy tổng 359 + 703 có kết quả ước lượng là: 400 + 700 = 1 100.
CM
2 tháng 1 2017
d. Số trung bình cộng: X = (7.4 + 8.8 + 9.10 + 10.8)/30 = 8,73 (1 điểm)
Mốt của dấu hiệu là: Mo = 9 (1 điểm)
CM
19 tháng 8 2017
Cách 1: x = n 1 x 1 + n 2 x 2 + n 3 x 3 + n 4 x 4 + n 5 x 5 n = 4 . 6 + 3 . 7 + 5 . 8 + 9 . 9 + 6 . 10 30 ≈ 8 , 33
Cách 2: Sử dụng máy tính Casio fx - 570 VNPLUS
+ Nhập 
(vào chế độ thống kê).
+ Nhập 
(hiển thị cột tần số).
+ Nhập 
(nhập giá trị).
+ Nhập 
, sau đó ấn 
.
+ Tính giá trị trung bình: Ấn 
⇒ x = 8 , 3333333 …
Đáp án A.
CM
31 tháng 3 2017
Cách 1:
+ Giá trị đại diện mỗi lớp: c 1 = 18 ; c 2 = 22 ; c 3 = 26 ; c 4 = 30 ; c 5 = 34
+ Số trung bình cộng:
x = n 1 c 1 + n 2 c 2 + n 3 c 3 + n 4 c 4 + n 5 c 5 n 1 + n 2 + n 3 + n 4 + n 5 = 10 . 18 + 12 . 22 + 14 . 26 + 9 . 30 + 5 . 34 50 ≈ 25
+ Độ lệch chuẩn:
s = s 2 = 10 18 - 25 2 + 12 22 - 25 2 + 14 26 - 25 2 + 9 30 - 25 2 + 5 34 - 25 2 50
≈ 5 , 0
Cách 2: Sử dụng máy tính Casio fx - 570 VNPLUS
+ Nhập 
(vào chế thống kê).
+ Nhập 
(hiển thị cột tần số).
+ Nhập 
(nhập giá trị).
+ Nhập 
(nhập tần số), sau đó ấn 
.
+ Nhập 
⇒ δ x = 4 , 983813801
(Lưu ý: Đối với Ví dụ 2, phương sai s 2 = 24 , 9 ).
Đáp án C.
HQ
Hà Quang Minh
Giáo viên
5 tháng 10 2023
+) Làm tròn số 479 633 tới hàng nghìn :
Chữ số ở hàng làm tròn là chữ số 9.
Chữ số ngay bên phải hàng làm tròn là 6 > 5 nên ta tăng chữ số hàng làm tròn thêm 1 đơn vị; các chữ số sau hàng làm tròn thuộc phần số nguyên nên ta thay bằng chữ số 0 . Khi đó ta được số làm tròn là: 480 000.
+) Làm tròn số 232,142 372 tới hàng đơn vị:
Chữ số ở hàng làm tròn là chữ số 2.
Chữ số ngay bên phải hàng làm tròn là 1 < 5 nên ta giữ nguyên chữ số ở hàng làm tròn; các chữ số sau hàng làm tròn thuộc phần thập phân nên ta bỏ đi hết . Khi đó ta được số làm tròn là: 232.
HQ
Hà Quang Minh
Giáo viên
26 tháng 9 2023
a)
Số trung bình \(\overline x = \frac{{8.1 + 19.10 + 20.19 + 21.17 + 22.3}}{{1 + 10 + 19 + 17 + 3}} = 20,02\)
+) Sắp xếp các giá trị theo thứ tự không giảm: \(8,\underbrace {19,...,19}_{10},\underbrace {20,...,20}_{19},\underbrace {21,...,21}_{17},22,22,22\)
Trung vị \({M_e} = \frac{1}{2}(20 + 20) = 20\)
+) Mốt \({M_o} = 20\)
b)
+) Tình độ lệch chuẩn:
Phương sai \({S^2} = \frac{1}{{50}}\left( {{8^2} + {{10.19}^2} + {{19.20}^2} + {{17.21}^2} + {{3.22}^2}} \right) - 20,{02^2} \approx 3,66\)
=> Độ lệch chuẩn \(S = \sqrt {{S^2}} \approx 1,91\)
+) Khoảng biến thiên \(R = 22 - 8 = 14\)
+) Tứ phân vị: \({Q_1},{Q_2},{Q_3}\)
\({Q_2} = {M_e} = 20\)
\({Q_1}\) là trung vị của mẫu: \(8,\underbrace {19,...,19}_{10},\underbrace {20,...,20}_{14}\). Do đó \({Q_1} = 20\)
\({Q_3}\) là trung vị của mẫu: \(\underbrace {20,...,20}_5,\underbrace {21,...,21}_{17},22,22,22\). Do đó \({Q_3} = 21\)
+) x là giá trị ngoại lệ nếu \(x > 21 + 1,5(21 - 20) = 22,5\) hoặc \(x < 20 - 1,5.(21 - 10) = 18,5\).
Vậy có một giá trị ngoại lệ là 8.
HQ
Hà Quang Minh
Giáo viên
8 tháng 10 2023
a) Hàng phần mười: -492,8; 320,1; -568,7
Hàng phần trăm: -492,79; 320,14; -568,72
Hàng phần nghìn: -492,793; 320,141; -568,718
b) Hàng đơn vị: -493; 320; -569
Hàng chục: -490; 320; -570
Hàng trăm: -500; 300; -600
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
Ta có:
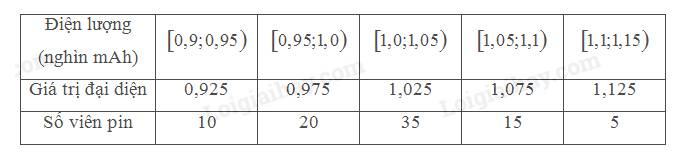
Tổng số viên pin là: \(n = 10 + 20 + 35 + 15 + 5 = 85\).
• Điện lượng trung bình của một số viên pin tiểu sau khi ghép nhóm là:
\(\bar x = \frac{{10.0,925 + 20.0,975 + 35.1,025 + 15.1,075 + 5.1,125}}{{85}} \approx 1,02\left( {mAh} \right)\)
• Nhóm chứa mốt của mẫu số liệu trên là nhóm \(\begin{array}{*{20}{c}}{\left[ {1,0;1,05} \right)}\end{array}\).
Do đó: \({u_m} = 1,0;{n_{m - 1}} = 20;{n_m} = 35;{n_{m + 1}} = 15;{u_{m + 1}} - {u_m} = 1,05 - 1,0 = 0,05\)
Mốt của mẫu số liệu ghép nhóm là:
\({M_O} = {u_m} + \frac{{{n_m} - {n_{m - 1}}}}{{\left( {{n_m} - {n_{m - 1}}} \right) + \left( {{n_m} - {n_{m + 1}}} \right)}}.\left( {{u_{m + 1}} - {u_m}} \right) = 1,0 + \frac{{35 - 20}}{{\left( {35 - 20} \right) + \left( {35 - 15} \right)}}.0,05 \approx 1,02\left( {mAh} \right)\)
Gọi \({x_1};{x_2};...;{x_{85}}\) là điện lượng của các viên pin được xếp theo thứ tự không giảm.
Ta có:
\(\begin{array}{l}{x_1},...,{x_{10}} \in \begin{array}{*{20}{c}}{\left[ {0,9;0,95} \right)}\end{array};{x_{11}},...,{x_{30}} \in \begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\left[ {0,95;1,0} \right)}\end{array}}\end{array};{x_{31}},...,{x_{65}} \in \begin{array}{*{20}{c}}{\left[ {1,0;1,05} \right)}\end{array};\\{x_{66}},...,{x_{80}} \in \begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\left[ {1,05;1,1} \right)}\end{array}}\end{array};{x_{81}},...,{x_{85}} \in \begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\left[ {1,1;1,15} \right)}\end{array}}\end{array}}\end{array}\end{array}\)
• Tứ phân vị thứ hai của dãy số liệu là: \({x_{43}}\)
Ta có: \(n = 85;{n_m} = 35;C = 10 + 20 = 30;{u_m} = 1,0;{u_{m + 1}} = 1,05\)
Do \({x_{43}} \in \begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\left[ {1,0;1,05} \right)}\end{array}}\end{array}}\end{array}\) nên tứ phân vị thứ hai của dãy số liệu là:
\({Q_2} = {u_m} + \frac{{\frac{n}{2} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 1,0 + \frac{{\frac{{85}}{2} - 30}}{{35}}.\left( {1,05 - 1,0} \right) \approx 1,02\)
• Tứ phân vị thứ nhất của dãy số liệu là: \(\frac{1}{2}\left( {{x_{21}} + {x_{22}}} \right)\).
Ta có: \(n = 85;{n_m} = 20;C = 10;{u_m} = 0,95;{u_{m + 1}} = 1,0\)
Do \({x_{21}},{x_{22}} \in \begin{array}{*{20}{c}}{\left[ {0,95;1,0} \right)}\end{array}\) nên tứ phân vị thứ nhất của dãy số liệu là:
\({Q_1} = {u_m} + \frac{{\frac{n}{4} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 0,95 + \frac{{\frac{{85}}{4} - 10}}{{20}}.\left( {1,0 - 0,95} \right) \approx 0,98\)
• Tứ phân vị thứ ba của dãy số liệu là: \(\frac{1}{2}\left( {{x_{64}} + {x_{65}}} \right)\).
Ta có: \(n = 85;{n_j} = 35;C = 10 + 20 = 30;{u_j} = 1,0;{u_{j + 1}} = 1,05\)
Do \({x_{64}},{x_{65}} \in \begin{array}{*{20}{c}}{\left[ {1,0;1,05} \right)}\end{array}\) nên tứ phân vị thứ ba của dãy số liệu là:
\({Q_3} = {u_j} + \frac{{\frac{{3n}}{4} - C}}{{{n_j}}}.\left( {{u_{j + 1}} - {u_j}} \right) = 1,0 + \frac{{\frac{{3.85}}{4} - 30}}{{35}}.\left( {1,05 - 1,0} \right) \approx 1,048\)
2 tháng 3 2022
1.Làm tròn số 92,117 đến hàng phần mười được kết quả là:92,1
2.Làm tròn số -845,654 đến hàng phần mười (đến chữ số thập phân thứ nhất) được kết quả là:-845,7
3.Làm tròn số 82,572 đến hàng phần mười được kết quả là:82,6
4.Làm tròn số 82,572 đến hàng phần mười được kết quả là:82,6
5.Làm tròn số -72,882 đến chữ số thập phân thứ nhất được kết quả là:-72,9
HQ
Hà Quang Minh
Giáo viên
8 tháng 10 2023
a) \( - 10,3;\,\,1995,9;\,\, - 822,4;\,\,100,\,0\)
b) \( - 10,35;\,\,1995,92;\,\, - 822,40;\,\,100,\,00\)
c) \( - 10;\,\,1996;\, - 822;\,100\)
d) \( - 10;\,2000;\,\, - 820;\,100\).
Để tính số trung bình và mốt của các tập dữ liệu đã cho, ta thực hiện như sau:
Tập dữ liệu A: 12; 32; 93; 78; 24; 12; 54; 66; 78
\(\text{S} \overset{ˊ}{\hat{\text{o}}} \&\text{nbsp};\text{trung}\&\text{nbsp};\text{b} \overset{ˋ}{\imath} \text{nh} = \frac{12 + 32 + 93 + 78 + 24 + 12 + 54 + 66 + 78}{9} = \frac{449}{9} \approx 49.89\)
(Làm tròn đến hàng phần trăm)
Tập dữ liệu B: 23; 41; 71; 29; 48; 45; 72; 41
\(\text{S} \overset{ˊ}{\hat{\text{o}}} \&\text{nbsp};\text{trung}\&\text{nbsp};\text{b} \overset{ˋ}{\imath} \text{nh} = \frac{23 + 41 + 71 + 29 + 48 + 45 + 72 + 41}{8} = \frac{370}{8} = 46.25\)
Kết luận:
Lưu ý rằng một tập dữ liệu có thể có một mốt, nhiều mốt hoặc không có mốt, tùy thuộc vào tần suất xuất hiện của các giá trị trong tập dữ liệu đó.