Cho tứ giác ABCD có điểm A, B cố định, còn điểm C, D di chuyển. Gọi O là giao điểm của AC và BD. Tỷ số OA/OC=a và OB/OD=b. (a, b khác 1). Chứng minh đường thẳng CD luôn đi qua một điểm cố định khi a khác b
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

CM
7 tháng 7 2018
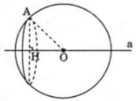
Gọi (P) là mặt phẳng đi qua A và vuông góc với đường thẳng a tại H. Khi đó (P) và H cố định.
Ta có: (P) cắt mặt cầu S(O; R) theo đường tròn tâm H và bán kính HA không đổi.
Vậy các mặt cầu tâm O bán kính R = OA luôn đi qua đường tròn cố định tâm H bán kính bằng HA.

CM
28 tháng 6 2017
Giả sử đường thẳng (k + 1)x – 2y = 1 đi qua điểm cố định M(x0; y0)
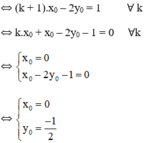
Vậy điểm cố định mà đường thẳng (k + 1)x – 2y = 1 đi qua là 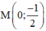

CM
20 tháng 2 2019
Giả sử đường thẳng (k + 1)x – 2y = 1 đi qua điểm cố định M ( x 0 ; y 0 )
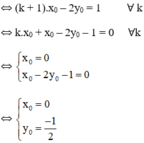
Vậy điểm cố định mà đường thẳng (k + 1)x – 2y = 1 đi qua là 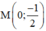
Giải chi tiết:
Bước 1: Xác định vị trí các điểm P, I, K, Q
Giả thiết:
Bước 2: Tính chất hình học
Bước 3: Tính diện tích PIKQ
\(S_{P I K Q} = \frac{1}{2} S_{A B C}\)
Ví dụ minh họa:
Cho tam giác ABC có diện tích \(20 \textrm{ } \text{cm}^{2}\).
\(S_{P I K Q} = \frac{1}{2} \times 20 = 10 \textrm{ } \text{cm}^{2}\)
Kết luận:
Diện tích tứ giác PIKQ bằng một nửa diện tích tam giác ABC nếu các điểm P, I, K, Q là trung điểm của các cạnh134.
Công thức tổng quát:
\(S_{P I K Q} = \frac{1}{2} S_{A B C}\)
Đáp án:
Diện tích tứ giác PIKQ là \(\boxed{\frac{1}{2} S_{A B C}}\).