Cho tam giác ABC có diện tích là 360m2
Biết AB = 3 x BM; AN = NP = PC; QB = QC
a, Tính diện tích tam giác AMN.
b, Tính diện tích hình MNPQB
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- So sánh được diện tích hình tam giác AMN bằng 1 2 diện tích hình tam giác ABN (Cùng đường cao từ B, cạnh đáy bằng nửa)
- So sánh được diện tích hình tam giác ABN bằng 1 2 diện tích hình tam giác ABC
- Kết luận diện tích hình tam giác AMN bằng 1 4 diện tích hình tam giác ABC

a: S AMB=S AMC=1/2*S ABC
S MNB=1/2*S AMB=1/4*S ABC
S MNC=1/2*S ANC=1/4*S ABC
=>S MNB=S MNC
b: Xét ΔABC có MN//BC
nên ΔANM đồng dạng với ΔABC
=>S ANM/ SABC=(AN/AB)^2=1/4
=>S ABC=24m2

Nối C với M
Tam giác ACM và tam giác ACB có chung đường cao hạ từ C xuống cạnh AB; đáy AM = 1/2 đáy AB (Vì M là điểm chính giữac cạnh AB)
=> S (ACM) = 1/2 S(ABC) = 1/2 x 160 = 80 cm2
Xét tam giác AMN và tam giác ACM có chung chiều cao hạ từ M xuống cạnh AC; đáy AN = 1/4 đáy AC
=> S (AMN) = 1/4 x S (ACM) = 1/4 x 80 = 20 cm2

\(AM=\dfrac{1}{2}AB\)
=>\(S_{AMC}=\dfrac{1}{2}\cdot S_{ABC}=\dfrac{1}{2}\cdot27=13,5\left(cm^2\right)\)
Vì \(AN=\dfrac{1}{3}AC\)
nên \(S_{AMN}=\dfrac{1}{3}\cdot S_{AMC}=\dfrac{1}{3}\cdot13,5=4,5\left(cm^2\right)\)

neu ai giai duoc cho minh bai nay thi minh se ve so do va nho cac cau giai ho
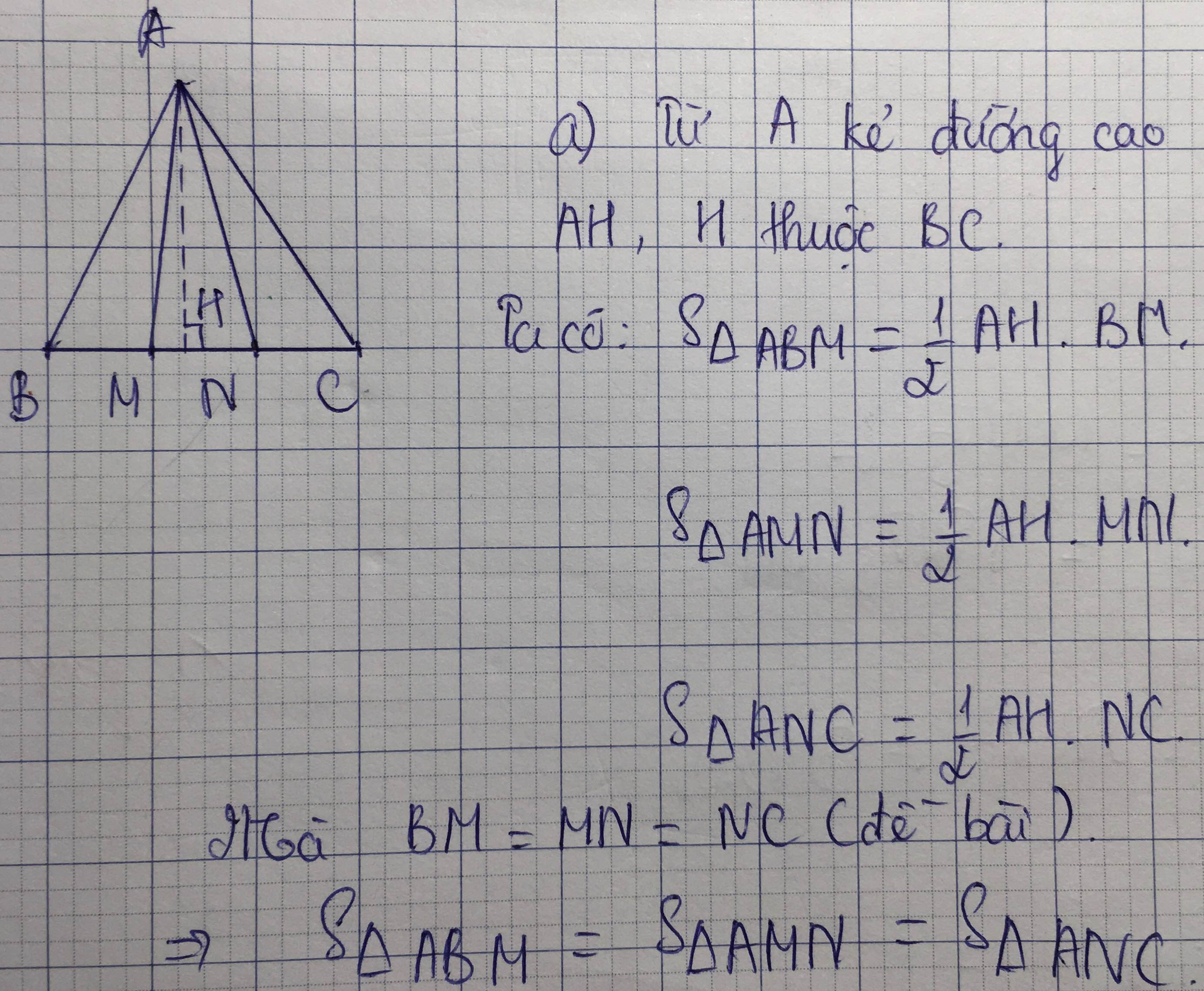

ai cíu tui dới
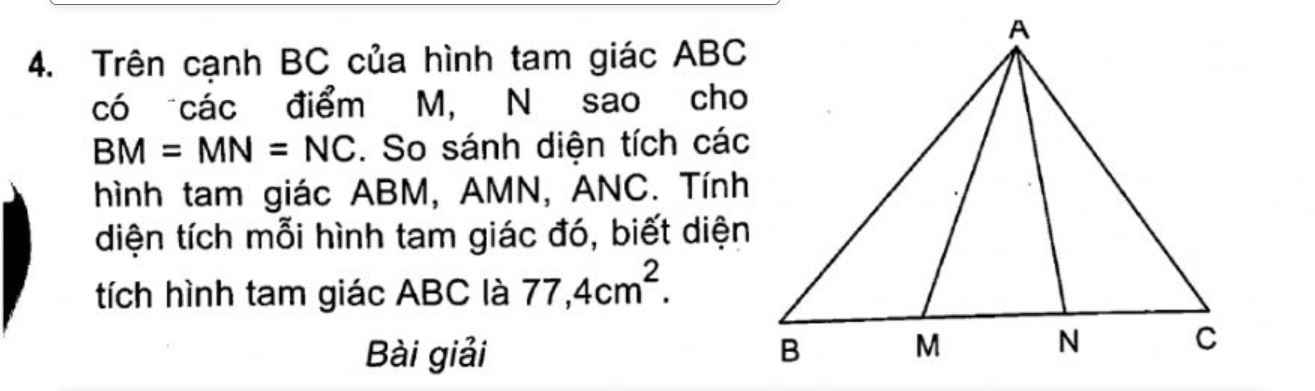
a. Tính diện tích tam giác AMN
Để tính diện tích của tam giác AMN, ta cần xét tỷ lệ các đoạn trong tam giác ABC và các phân đoạn chia đều.
Vì \(A B = 3 \times B M\) và \(A N = N P = P C\), ta có tỷ lệ diện tích của tam giác AMN so với tam giác ABC là:
\(\text{T}ỷ\&\text{nbsp};\text{l}ệ\&\text{nbsp};\text{di}ệ\text{n}\&\text{nbsp};\text{t} \overset{ˊ}{\imath} \text{ch}\&\text{nbsp};\text{AMN} = \frac{1}{3} \times \frac{1}{3} = \frac{1}{9}\)
\(\text{Di}ệ\text{n}\&\text{nbsp};\text{t} \overset{ˊ}{\imath} \text{ch}\&\text{nbsp};\text{tam}\&\text{nbsp};\text{gi} \overset{ˊ}{\text{a}} \text{c}\&\text{nbsp};\text{AMN} = \frac{1}{9} \times 360 = 40 \textrm{ } \text{m}^{2}\)
b. Tính diện tích hình MNPQB
Để tính diện tích của hình MNPQB, ta sẽ trừ diện tích của các phần nhỏ ra khỏi diện tích tam giác ABC. Các phần này bao gồm tam giác AMN và các tam giác nhỏ khác mà ta cần tính diện tích.
Diện tích của các phần nhỏ là: \(360 - 40 = 320 \textrm{ } \text{m}^{2}\).
Vậy, diện tích của hình MNPQB là 320 m².
Tóm lại: a) Diện tích tam giác AMN là 40 m².
b) Diện tích hình MNPQB là 320 m².