Chứng minh: Nếu a2 + b2 chia hết cho 5 thì hai số 2a – b và 2b + a hoặc 2a + b và 2b – a chia hết cho 5.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan
PA
0


CM
9 tháng 12 2018
Đáp án D

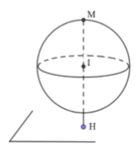
Bài toán trở thành: Tìm M nằm trên đường tròn giao tuyến của mặt cầu (S) và mặt phẳng (P) sao cho KM lớn nhất






24 tháng 8 2021
c: Ta có: \(a\left(a+2b\right)^3-b\left(2a+b\right)^3\)
\(=a^4+6a^3b+12a^2b^2+8ab^3-8a^3b-12a^2b^2-6ab^3-b^4\)
\(=a^4-2a^3b+2ab^3-b^4\)
\(=\left(a-b\right)\left(a+b\right)\left(a^2+b^2\right)-2ab\left(a^2-b^2\right)\)
\(=\left(a-b\right)^3\cdot\left(a+b\right)\)

28 tháng 7 2021
a) Ta có: \(N=a^2+b^2+2a-b-\dfrac{1}{4}\)
\(=a^2+2a+1+b^2-b+\dfrac{1}{4}-\dfrac{3}{2}\)
\(=\left(a+1\right)^2+\left(b-\dfrac{1}{2}\right)^2-\dfrac{3}{2}\ge-\dfrac{3}{2}\forall a,b\)
Dấu '=' xảy ra khi a=-1 và \(b=\dfrac{1}{2}\)



Ta có:
(2a - b)(2a + b) = 4a^2 - b^2 = 5a^2 - (a^2 + b^2)
(2b + a)(2b - a) = 4b^2 - a^2 = 5b^2 - (a^2 + b^2)
Vì : 5a^2 , 5b^2 và (a^2 + b^2) chia hết cho 5
thì (2a - b)(2a + b) chia hết cho 5
và (2b + a)(2b - a) chia hết cho 5
mà 5 là số nguyên tố
nên: 2a - b và 2b + a hoặc 2a + b và 2b - a chia hết cho 5 (đpcm)