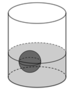
Một cốc nước dạng hình trụ có chiều cao 12 cm, bán kính đáy 2cm, lượng nước trong cốc cao8cm.
a) Tính thể tích tối đa mà cốc có thể chứa.
b) Người ta thả vào cốc nước 6viên bi hình cầu có cùng bán kính 1cm và ngập hoàn toàn trong nước, làm nước trong cốc dâng lên. Hỏi sau khi thả 6 viên bi vào thì mực nước trong cốc cách miệng cốc bao nhiên xentimet? (Giả sử độ dày của cốc là không đáng kể).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

cho mình hỏi chỗ v1 sao lại là 5 . \(\dfrac{4}{3}\pi R^3\) vậy ạ

Thể tích khối nước trong cốc là
![]()
Thể tích của khối cầu là 4 3 πR 3
Sau khi thả viên bi, chiều cao của mực nước bằng đường kính khối cầu nên tổng thể tích của nước và khối cầu là
![]()
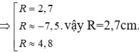
vậy R=2,7cm.
Chọn đáp án D.

Chọn đáp án D.
Thể tích khối nước trong cốc là:
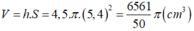
Thể tích của khối cầu là 4 3 π R 3 .
Sau khi thả viên bi, chiều cao của mực nước bằng đường kính khối cầu nên tổng thể tích của nước và khối cầu là:
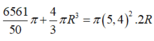
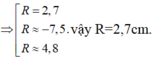

.V=100cm3=100.10−6=10−4(m3)V=100cm3=100.10−6=10−4(m3)
khi khối đá cân bằng
P=FA⇒10DV=dnVc⇒10.920.10−4=10000.Vc⇒Vc=9,2.10−5(m3)P=FA⇒10DV=dnVc⇒10.920.10−4=10000.Vc⇒Vc=9,2.10−5(m3)
.Vc=9,2.10−5m3=92cm3Vc=9,2.10−5m3=92cm3

Thể tích khối trụ ![]() Suy ra thể tích lượng nước
Suy ra thể tích lượng nước ![]()
Từ giả thiết suy ra thể tích khối cầu:
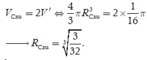
Vậy diện tích xung quanh của khối cầu là ![]()
Chọn C.




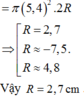


a) Tính thể tích tối đa mà cốc có thể chứa:
Cốc nước có dạng hình trụ, vì vậy thể tích của cốc sẽ được tính bằng công thức thể tích của hình trụ:
\(V_{\text{c} \overset{ˊ}{\hat{\text{o}}} \text{c}} = \pi r^{2} h\)
Trong đó:
Cho trước:
Áp dụng công thức:
\(V_{\text{c} \overset{ˊ}{\hat{\text{o}}} \text{c}} = \pi \times 2^{2} \times 12 = \pi \times 4 \times 12 = 48 \pi \textrm{ } \text{cm}^{3}\)
Vậy thể tích tối đa mà cốc có thể chứa là:
\(V_{\text{c} \overset{ˊ}{\hat{\text{o}}} \text{c}} = 48 \pi \approx 150.8 \textrm{ } \text{cm}^{3}\)
b) Tính mực nước sau khi thả 6 viên bi vào cốc:
Bước 1: Tính thể tích của 6 viên bi:
Viên bi có dạng hình cầu, thể tích của một viên bi được tính theo công thức:
\(V_{\text{bi}} = \frac{4}{3} \pi r^{3}\)
Trong đó:
Cho trước bán kính viên bi là 1 cm, nên thể tích của một viên bi là:
\(V_{\text{bi}} = \frac{4}{3} \pi \times 1^{3} = \frac{4}{3} \pi \textrm{ } \text{cm}^{3}\)
Vậy thể tích của 6 viên bi là:
\(V_{\text{6}\&\text{nbsp};\text{bi}} = 6 \times \frac{4}{3} \pi = 8 \pi \textrm{ } \text{cm}^{3}\)
Bước 2: Tính mực nước dâng lên trong cốc:
Lượng nước trong cốc sẽ tăng lên do thể tích của các viên bi thả vào. Mỗi viên bi chiếm một thể tích của nước, nên mực nước trong cốc sẽ dâng lên một lượng nhất định.
Giả sử sau khi thả vào, mực nước dâng lên một khoảng \(h_{\text{d} \hat{\text{a}} \text{ng}}\). Mực nước này sẽ tạo thành một hình trụ có bán kính đáy là 2 cm và chiều cao là \(h_{\text{d} \hat{\text{a}} \text{ng}}\). Thể tích của phần nước dâng lên này chính là thể tích của 6 viên bi, tức là \(8 \pi \textrm{ } \text{cm}^{3}\).
Áp dụng công thức thể tích hình trụ để tính mực nước dâng lên:
\(V_{\text{d} \hat{\text{a}} \text{ng}} = \pi r^{2} h_{\text{d} \hat{\text{a}} \text{ng}}\)
Trong đó:
Thể tích nước dâng lên là \(8 \pi\), nên ta có:
\(8 \pi = \pi \times 2^{2} \times h_{\text{d} \hat{\text{a}} \text{ng}}\) \(8 \pi = 4 \pi \times h_{\text{d} \hat{\text{a}} \text{ng}}\)
Chia cả hai vế cho \(\pi\):
\(8 = 4 \times h_{\text{d} \hat{\text{a}} \text{ng}}\) \(h_{\text{d} \hat{\text{a}} \text{ng}} = 2 \textrm{ } \text{cm}\)
Kết quả:
Sau khi thả 6 viên bi vào cốc, mực nước trong cốc dâng lên 2 cm. Do đó, mực nước cách miệng cốc là:
\(12 - 8 - 2 = 2 \textrm{ } \text{cm}\)
Vậy mực nước cách miệng cốc 2 cm.