Question

[Hiếu Hạnh Nguyễn]

Cho x,y,z thuộc R thỏa mãn x+y+z=0 và -1 ≤ x ≤ 1; -1 ≤ y ≤ 1; -1 ≤ z ≤ 1. Chứng minh: x^2 + y^4 + z^6 có giá trị ≤ 2

Answer 1

[trần doãn thành]

• Do \(- 1 \leq x \leq 1\) nên \(x^{2} \leq 1\).
• Do \(- 1 \leq y \leq 1\) nên \(y^{4} \leq 1\).
• Do \(- 1 \leq z \leq 1\) nên \(z^{6} \leq 1\).

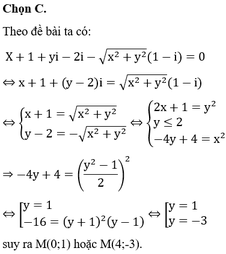
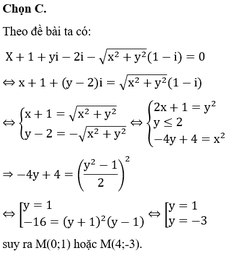
Như vậy, tổng lớn nhất của các số này có thể đạt tới:

\(x^{2} + y^{4} + z^{6} \leq 1 + 1 + 1 = 3.\)

Tuy nhiên, ta cần chứng minh rằng nó không thể vượt quá 2.

z=−(x+y).

Thay vào biểu thức cần chứng minh:

\(x^{2} + y^{4} + \left(\right. - \left(\right. x + y \left.\right) \left.\right)^{6} .\)

Tìm giá trị lớn nhất của \(x^{2} + y^{4} + z^{6}\)

Ta xét một số trường hợp đặc biệt:

1. Trường hợp \(x = 1 , y = - 1 , z = 0\):
   \(x^{2} + y^{4} + z^{6} = 1^{2} + \left(\right. - 1 \left.\right)^{4} + 0^{6} = 1 + 1 + 0 = 2.\)
   Như vậy, giá trị này có thể đạt tới 2.
2. Trường hợp \(x = 1 , y = 0 , z = - 1\):
   \(x^{2} + y^{4} + z^{6} = 1^{2} + 0^{4} + \left(\right. - 1 \left.\right)^{6} = 1 + 0 + 1 = 2.\)
   Giá trị này cũng là 2.
3. Do các giá trị cao nhất của mỗi số hạng không thể đồng thời lớn hơn 1 trong điều kiện \(x + y + z = 0\), tổng giá trị tối đa của chúng chỉ có thể đạt 2.
4. x2+y4+z6≤2.

Dấu "=" xảy ra khi \(\left(\right. x , y , z \left.\right)\) nhận các giá trị như \(\left(\right. 1 , - 1 , 0 \left.\right)\) ; (1,0,-1) ; (0,-1,1) ; (0,1,-1) ; (-1,0,1) ; (-1,1,0)