(1,5 điểm) Cho sơ đồ chuyển hóa sau:a) Hoàn thành sơ đồ trên.b) Phức chất nào trong sơ đồ trên có dạng bát...
Đọc tiếp
(1,5 điểm) Cho sơ đồ chuyển hóa sau:
a) Hoàn thành sơ đồ trên.
b) Phức chất nào trong sơ đồ trên có dạng bát diện?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
3 tháng 6 2018
%Na = 39,316% => MZ = 58,5
=> Z là NaCl
=> X là H2 và Y là HCl
Pt: Cl2 + H2 → 2HCl
HCl + NaOH → NaCl + H2O
2NaCl + H2SO4đặc → Na2SO4 + 2HCl
4HCl + MnO2 → MnCl2 + Cl2↑ + 2H2O
10 tháng 3 2022
A: CaCO3
B: CO2
C: NaHCO3
D: Na2CO3
E: HCl
F: CaCl2
PTHH:
\(CaCO_3\left(A\right)\underrightarrow{t^o}CaO+CO_2\left(B\right)\)
\(CO_2\left(B\right)+NaOH\rightarrow NaHCO_3\left(C\right)\)
\(CO_2\left(B\right)+2NaOH\rightarrow Na_2CO_3\left(D\right)+H_2O\)
\(NaHCO_3\left(C\right)+HCl\left(E\right)\rightarrow NaCl\left(H\right)+CO_2+H_2O\)
\(Na_2CO_3\left(D\right)+CaCl_2\left(F\right)\rightarrow2NaCl\left(H\right)+CaCO_3\downarrow\)
\(NaHCO_3\left(C\right)+NaOH\rightarrow Na_2CO_3\left(D\right)+H_2O\)
\(Na_2CO_3\left(D\right)+HCl\rightarrow NaCl+NaHCO_3\left(E\right)\)
LN
0
NH
1
5 tháng 6 2018
- Sơ đồ:
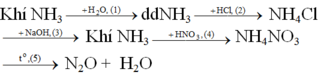
Phương trình phản ứng:
(1) Khí NH3 + H2O ⇆ NH4OH
(2) NH3 + HCl → NH4Cl
(3) NH4Cl + NaOH → NH3↑ + NaCl + H2O
(4) NH3 + HNO3 → NH4NO3
(5) NH4NO3 → N2O + 2H2O
17 tháng 8 2021
A : Fe , B : O2 , C : Zn , D : HCl , E : O2
a) 3Fe + 2O2 → (to) Fe3O4
b) S + O2 → (to) SO2
c) Zn + H2SO4 → ZnSO4 + H2
d) HCl + KOH → KCl + H2O
e) 2HgO → (to) O2 + 2Hg
Chúc bạn học tốt
PL
9 tháng 4 2023
Từ A tạo ra cao su ⇒ A phải thuộc dãy đồng đẳng ankađien liên hợp.
⇒ C4H6 trong TH này là Buta-1,3-đien.
(1) \(\left[{}\begin{matrix}CH_2=CH-CH=CH_2+Cl_2\rightarrow CH_2Cl-CHCl-CH=CH_2\left(\text{Cộng 1,2}\right)\\CH_2=CH-CH=CH_2+Cl_2\rightarrow CH_2Cl-CH=CH-CH_2Cl\left(\text{Cộng 1,4}\right)\end{matrix}\right.\)
➤ Note: Từ các pthh dưới mình lấy sp cộng 1,4. Sản phẩm cộng 1,2 viết tương tự.
(2) \(CH_2Cl-CH=CH-CH_2Cl+NaOH\rightarrow CH_2\left(OH\right)-CH=CH-CH_2\left(OH\right)\)
(3) \(CH_2\left(OH\right)-CH=CH-CH_2\left(OH\right)\xrightarrow[Ni]{t^\circ}CH_2\left(OH\right)-CH_2-CH_2-CH_2\left(OH\right)\)(4) \(CH_2\left(OH\right)-CH_2-CH_2-CH_2\left(OH\right)\xrightarrow[H_2SO_4\left(đ\right)]{170^\circ C}CH_2=CH-CH=CH_2+2H_2O\)
(5) \(nCH_2=CH-CH=CH_2\xrightarrow[xt]{t^\circ,p}\left(-CH_2-CH=CH-CH_2\right)_n\)
