1. Vẽ n điểm phân biệt, chúng tạo ra 190 đoạn thẳng. Tìm giá trị của n .
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CC
28 tháng 12 2019
Từ 1 điểm trong n điểm trên tia Ox tạo với các điểm còn lại số đoạn thẳng là: \(n-1\)đoạn thẳng
Làm tương tự với các điểm còn lại ta có số đoạn thẳng là: \(n\left(n-1\right)\)đoạn thẳng
Mà mỗi đoạn thẳng trùng nhau 2 lần nên số đoạn thẳng thực có là: \(\frac{n\left(n-1\right)}{2}\)đoạn thẳng
Theo đề bài ta có: \(\frac{n\left(n-1\right)}{2}=190\)\(\Rightarrow n\left(n-1\right)=380=20.19\)\(\Rightarrow n=20\)
Vậy \(n=20\)
CM
13 tháng 11 2017
Đáp án D
Số cách chọn ra 3 điểm từ 2n điểm đã cho là C 2 n 3 suy ra số mặt phẳng được tạo ra là C 2 n 3 .
Do trong 2n điểm đã cho có n điểm đồng phẳng nên có C n 3 mặt phẳng trùng nhau.
Suy ra số mặt phẳng được tạo thành từ 2n điểm đã cho là C 2 n 3 − C n 3 + 1 .
PN
18 tháng 10 2017
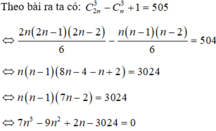
Vi: \(n\ge2\)
Số điểm cho trước có công thức tính dạng chung là: 2x với \(x\in N\)
Áp dụng công thức tính đoạn thẳng, ta có:
\(\frac{2x.2x-1}{2}=x.2x-1=2x^2-2\)
Vậy: Có tất cả là: 2x2 - x
Công thức tính:
\(\frac{n.n-1}{2}\)với n là số điểm cho trước
29 tháng 1 2018
Áp dụng công thức:
\(\frac{n\left(n-1\right)}{2}\)
Vậy khi đó giá trị của n là:
\(\frac{190\left(190-1\right)}{2}\)= 17955 ( điểm )
Đ/S: 17955 điểm
17 tháng 10 2017
Lấy 1 điểm trong n điểm phân biệt nối với n - 1 điểm còn lại ta được ( n - 1 ) đoạn thẳng. Cứ làm như vậy với n - 1 điểm còn lại ta được n( n - 1 ) đoạn thẳng. Nhưng làm như vậy, số đoạn thẳng sẽ được tính 2 lần. Vậy số đoạn thẳng thực tế là: n.( n - 1 ) : 2 đoạn thẳng.
Theo đề bài, ta có: n. ( n - 1 ) : 2 = 120
suy ra n. ( n - 1 ) = 120 . 2 = 240
suy ra n. ( n - 1 ) = 15.16
Vậy n = 16
Nhớ k cho mình nhé! Thank you!!!
Mk lm theo cách của mk nha !
Nối 1 điểm với n-1 điểm còn lại ta được n-1 đoạn thẳng.
Làm như vậy với n điểm ta có :
n . ( n-1) ( đoạn thẳng )
Nhưng mỗi đoạn thẳng đc tính hai lần nên với n điểm ta có số đoạn thẳng là : \(\frac{n.\left(n-1\right)}{2}\) (đoạn thẳng )
Ta có :
\(\frac{n.\left(n-1\right)}{2}\) = 190
n.(n-1) = 190.2
n.(n-1) = 380
n.(n-1) = 20.19
=> n = 20
Vậy số điểm cần tìm là 20