Cho góc nhọn xOy, trên tia Ox lấy điểm A,C, trên tia Oy lấy điểm B,D sao cho OA = OB, OC = OD.
a) Chứng minh ΔOAD = ΔOBC
b)Chứng minh ∠CAD = ∠CBD
( Δ : tam giác ) ( ∠ : góc )
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

O A C B D x y
a) Xét tam giác OAD và OBC có: OA = OB; góc BOC chung; OD = OC
=> tam giác OAD = OBC ( c - g - c)
=> góc OAD = OBC
Mà góc CAD = 180o - OAD; góc CBD = 180o - OBC
Nên góc CAD = góc CBD


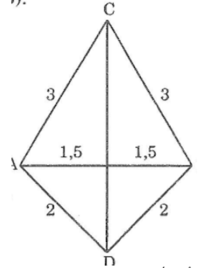
Xét ΔCAD và ΔCBD, ta có:
AC = BC (= 3 cm)
AD = BD (= 2 cm)
CD cạnh chung
Suy ra: ΔCAD= ΔCBD(c.c.c)
Vậy ∠(CAD) =∠(CBD) ̂(hai góc tương ứng)

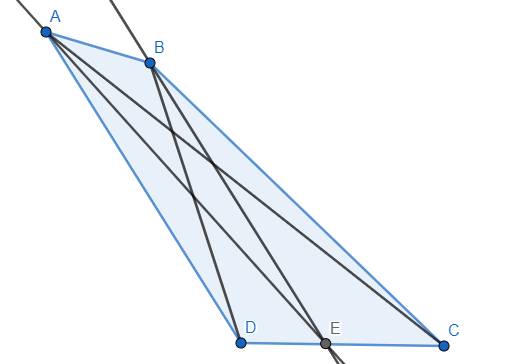
Áp dụng tính chất tia phân giác, ta có \(\dfrac{ED}{EC}=\dfrac{AD}{AC}\) và \(\dfrac{ED}{EC}=\dfrac{BD}{BC}\). Từ đó suy ra \(\dfrac{AD}{AC}=\dfrac{BD}{BC}\Rightarrow AD.BC=AC.BD\) (đpcm)

xét 2 tam giác ACD và BCD có AD=BD=2cm, AC=BC=3cm, CD chung
=> tg ACD= tg BCD (c.c.c) =>góc CAD= góc CBD

Xét tam giác ABC và tam giác ABD, có:
AC=CD ( gt )
CD là cạnh chung
AD=BD ( gt )
Vậy CAD=CBD (c.c.c )
a: Xét ΔOAD và ΔOBC có
OA=OB
\(\widehat{AOD}\) chung
OD=OC
Do đó: ΔOAD=ΔOBC
b: ΔOAD=ΔOBC
=>\(\widehat{OAD}=\widehat{OBC}\)
mà \(\widehat{OAD}+\widehat{DAC}=180^0\)(hai góc kề bù)
và \(\widehat{OBC}+\widehat{CBD}=180^0\)(hai góc kề bù)
nên \(\widehat{DAC}=\widehat{CBD}\)
a) Chứng minh ΔOAD = ΔOBC
b) Chứng minh ∠CAD = ∠CBD