K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 2 2023
a: Xét tứ giác ADKE có
AE//DK
AE=DK
góc EAD=90 độ
=>ADKE là hình chữ nhật
b: Xét tứ giác AECK có
AE//CK
AE=CK
=>AECK là hình bình hành
=>AK//EC
=>AK vuông góc DM
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 9 2021
\(\left\{{}\begin{matrix}AM=\sqrt{AB^2+BM^2}=3\sqrt{5}\\DM=\sqrt{CD^2+CM^2}=3\sqrt{5}\end{matrix}\right.\) \(\Rightarrow\) tam giác ADM cân tại M
Gọi F là trung điểm AD \(\Rightarrow ABMF\) là hình chữ nhật \(\Rightarrow MF=AB=6\)
Theo tính chất trọng tâm: \(GF=\dfrac{1}{3}MF=2\)
\(DF=\dfrac{1}{2}AD=3\)
Đặt \(T=\left|\overrightarrow{GD}\right|=\left|\overrightarrow{GF}+\overrightarrow{FD}\right|\)
\(\Rightarrow T^2=GF^2+FD^2+2\overrightarrow{GF}.\overrightarrow{DF}=GF^2+DF^2=2^2+3^2=13\)
\(\Rightarrow\left|\overrightarrow{GD}\right|=\sqrt{13}\)
15 tháng 6 2018
A B C D E M N O
a) Chu vi hình chữ nhật là :
\(\left(10+6\right)\times2=32\left(cm\right)\)
Do hình vuông có chu vi bằng chu vi hình chữ nhật ấy nên chu vi của hình vuông ABCD là 32 cm
Cạnh hình vuông là :
\(32\div4=8\left(cm\right)\)
b) Do M là điểm chính giữa cạnh AB nên \(AM=MB=\frac{AB}{2}=4\left(cm\right)\)
Ta có \(S_{\Delta ADM}=\frac{AD\times AM}{2}=\frac{8\times4}{2}=16\left(cm^2\right)\)
Do N là điểm chính giữa cạnh BC nên \(BN=NC=\frac{BC}{2}=4\left(cm\right)\)
\(S_{\Delta ABN}=\frac{AB\times BN}{2}=\frac{8\times4}{2}=16\left(cm^2\right)\)
Xét \(\Delta ABN\)và \(\Delta AMN\)có chung đường cao hạ từ N xuống cạnh đáy
Mà đáy AM của \(\Delta AMN\) \(=\frac{1}{2}\)đáy AB của \(\Delta ABN\)
\(\Rightarrow S_{\Delta AMN}=\frac{1}{2}S_{\Delta ABN}=\frac{1}{2}\times16=8\left(cm^2\right)\)
Kẻ \(NO\perp AD\)
Xét tứ giác ABNO có \(\widehat{OAB}=\widehat{ABN}=\widehat{NOA}=90^o\)
\(\Rightarrow\) ABNO là hình chữ nhật
\(\Rightarrow NO=AB=8\left(cm\right)\)
\(S_{\Delta AND}=\frac{NO\times AD}{2}=\frac{8\times8}{2}=32\left(cm^2\right)\)
Vậy ...
PT
6 tháng 2 2021
xét ΔADM và ΔADN có:
AD chung
MAD=NAD(góc)
AMD=AND=90(góc)
⇒ΔADM=ΔADN(cạnh huyền--góc nhọn)
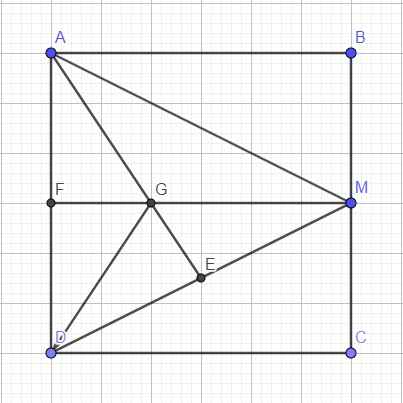
a: Gọi I là giao điểm của AF và DM
Ta có: \(AE=EB=\dfrac{AB}{2}\)
\(DF=FC=\dfrac{DC}{2}\)
mà AB=DC(ABCD là hình vuông)
nên AE=EB=DF=FC
Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành
=>AF//CE
mà DM\(\perp\)CE
nên DM\(\perp\)AF tại I
Xét ΔDMC có
F là trung điểm của DC
FI//MC
Do đó: I là trung điểm của DM
XétΔADM có
AI là đường cao
AI là đường trung tuyến
Do đó: ΔADM cân tại A