Cho ba hình chữ nhật, biết diện tích của hình thứ nhất và diện tích của hình thứ hai tỉ lệ với 4 và 5, diện tích hình thư hai và diện tích hình thứ ba tỉ lệ với 7 và 8, hình thứ nhất và hình thứ hai có cùng chiều dài và tổng các chiều rộng của chúng là 27 cm, hình thứ hai và hình thứ ba có cùng chiều rộng, chiều dài của hình thứ ba là 24 cm. Tính diện tích của mỗi hình chữ nhật đó.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Gọi kích thước của hình hộp CN là $a,b,c$ (cm) thì theo bài ra ta có:
\(\frac{a}{6}=\frac{b}{8}=\frac{c}{10}; abc=3840\)
\(\Rightarrow (\frac{a}{6})^3=(\frac{b}{8})^3=(\frac{c}{10})^3=\frac{a}{6}.\frac{b}{8}.\frac{c}{10}=\frac{abc}{480}=8\)
\(\Rightarrow \frac{a}{6}=\frac{b}{8}=\frac{c}{10}=2\Rightarrow a=12; b=16; c=20\) (cm)
Diện tích toàn phần của hình hộp chữ nhật:
\(S_{tp}=2(ab+bc+ac)=2(12.16+16.20+12.20)=1504\) (cm vuông)

Nửa chu vi hình chữ nhật là : 70 : 2 = 35
Gọi chiều dài là a ; chiều rộng là b (a > b)
Theo bài ra ta có : a + b = 35
\(\frac{a}{5}=\frac{b}{2}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có :
\(\frac{a}{5}=\frac{b}{2}=\frac{a+b}{5+2}=\frac{35}{7}=5\)
=> a = 25 ; b = 10
Vậy chiều dài là 25 cm; chiều rộng là 10 cm

Nửa chi vi của hình chữ nhật đó là:
30 : 2 =15 (cm)
Gọi kích thước của chiều rộng và chiều dài của hình chữa nhật đó là a,b ( a,b >0 ) (cm) .
Theo bài ra , ta có:
\(\frac{a}{2}=\frac{b}{3}\)và a+b=15
Áp dụng tính chất của dãy tỉ số bằng nhau có:
\(\frac{a}{2}=\frac{b}{3}=\frac{a+b}{2+3}=\frac{15}{5}=3\)
=> a = 3.2 = 6
b = 3.3 = 9
Vậy diện tích hình chữ nhật đó là:
6 . 9 = 54( cm2 )
Học tốt

Gọi độ 2 cạnh chữ nhật là a,b (a,b>0)
Theo bài ra ta có:\(\left\{{}\begin{matrix}\dfrac{a}{3}=\dfrac{b}{4}\\ab=300\end{matrix}\right.\)
Đặt \(\dfrac{a}{3}=\dfrac{b}{4}=k\left(k>0\right)\Rightarrow a=3k,b=4k\)
\(ab=300\\ \Rightarrow3k.4k=300\\ \Rightarrow12k^2=300\\ \Rightarrow k^2=25\\ \Rightarrow k=5\left(vìk>0\right)\\ \Rightarrow\left\{{}\begin{matrix}a=15\\b=20\end{matrix}\right.\)

Bài giải
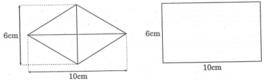
Tính tỉ số diện tích giữa hình thoi và hình chữ nhật
Diện tích hình thoi là: 1 2 × 6 × 10 = 30 c m 2
Diện tích hình chữ nhật là: 10 × 6 = 60 c m 2
Tỉ số diện tích giữa hình thoi và hình chữ nhật là: 30 : 60 = 1 2

Gọi chiều rộng là \(x\left(cm\right)\)
chiều dài là \(y\left(cm\right)\)
Ta có
\(x:y=3:5\\ =>\dfrac{x}{3}=\dfrac{y}{5}\)
Diện tích là \(x\times y=240\left(m^2\right)\)
Áp dụng tính chất dãy tỉ số bằng nhau:
\(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{x\times y}{3\times5}=\dfrac{240}{15}=16\)
\(\Rightarrow\) chiều rộng là \(16\times3=48\left(m\right)\)
Chiều dài là \(16\times5=80\left(m\right)\)
Chu vi : \(\left(48+80\right)\times2=256\left(m\right)\)
Trước khi làm bài này, hãy chú ý rằng:
\(\dfrac{a}{b}=\dfrac{c}{d}\) thì chưa chắc \(\dfrac{a}{b}=\dfrac{c}{d}=\dfrac{ac}{bd}\)
Gọi chiều dài và chiều rộng hình chữ nhật lần lượt là \(a,b\left(a>b\right)\)
Thèo bài toán, ta có:
\(\dfrac{a}{5}=\dfrac{b}{3}\) và \(ab=240\)
Gọi \(k\) sao cho \(\dfrac{a}{5}=\dfrac{b}{3}=k\)
Khi đó:
\(\left\{{}\begin{matrix}a=5k\\b=3k\end{matrix}\right.\)
\(\Rightarrow ab=5k\cdot3k=15k^2=240\)
\(\Rightarrow k^2=240:15=16\)
\(\Rightarrow k=4\)
Vậy \(\left\{{}\begin{matrix}a=3\cdot4=12\\b=5\cdot4=20\end{matrix}\right.\)


Gọi: Chiều dài là x, chiều rộng là y
Theo đề bài ra, ta có: \(\frac{S_1}{S_2}=\frac45;\frac{S_2}{S_3}=\frac78;x_1=x_2;y_1+y_2=27;y_2=y_3;x_3=24\)
Mà \(x_1=x_2;\frac{S_1}{S_2}=\frac45\Rightarrow\frac{y_1}{y_2}=\frac45\)
Vậy: Chiều rộng của hình chữ nhật thứ nhất là: \(\frac{27}{\left(4+5\right)}\times4=12\left(\operatorname{cm}\right)\)
Chiều rộng của hình chữ nhật thứ hai hoặc ba là: \(27-12=15\left(\operatorname{cm}\right)\)
Diện tích của hình chữ nhật thứ 3 là: \(15\times24=360\left(\operatorname{cm}\right)\)
Diện tích của hình chữ nhật thứ 2 là: \(360\times\frac78=315\left(\operatorname{cm}\right)\)
Diện tích của hình chữ nhật thứ 1 là: \(315\times\frac45=252\left(\operatorname{cm}\right)\)