Cho n điểm phân biệt.Kẻ các đường thẳng đi qua các cặp điểm trong n điểm đã cho.Biết có tất cả 190 đường thẳng tạo thành.Tìm n
Cứu tôi với(ToT)(ToT)(ToT)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PM
31 tháng 12 2017
ta có qua 2 điểm ta vẽ được 1 đường thẳng
3điểm ta vẽ được 2đương thẳng
n điểm ta vẽ được n(n-1):2 đường thẳng
16 tháng 12 2019
chon n diem noi voi n-1 diem con lai, ta dc n-1 duong thang
co tat ca n diem nhu the nen so duong thang la n.(n-1) (duong thang)
nhung moi duong thang duoc tinh 2 lan nen so duong thang thuc su co la: \(\frac{n.\left(n-1\right)}{2}\)(duong thang)
16 tháng 12 2019
Gọi n điểm đã cho là: \(A_1;A_2;A_3;...;A_n\); n\(\ge\)2.
Vì không có 3 điểm nào thẳng hàng nên :
+) Nối \(A_1\) với ( n - 1) điểm còn lại ta có: ( n - 1) đường thẳng.
+) Nối \(A_2\) với ( n - 1) điểm còn lại ta có: ( n - 1) đường thẳng.
+) Nối \(A_3\) với ( n - 1) điểm còn lại ta có: ( n - 1) đường thẳng.
...
+) Nối \(A_3\) với ( n - 1) điểm còn lại ta có: ( n - 1) đường thẳng.
Như chúng ta có: n ( n - 1) đường thẳng
Tuy nhiên mỗi đường thẳng được tính 2 lần ( VD như nối \(A_1\)với \(A_2\)ta có đường thẳng \(A_1\)\(A_2\); còn nối \(A_2\)với \(A_1\)ta có đường thẳng \(A_2\)\(A_1\); và 2 đường thẳng \(A_1\)\(A_2\); \(A_2\)\(A_1\) trùng nhau )
=> Do đó số đường thẳng phân biệt là: n ( n - 1) : 2.
19 tháng 11 2017
a,n.(n-1):2
b,n.(n-1):2=28 suy ran.(n-1)=56 suy ra n và n-1 là hai số tự nhiên liên tiếp suy ra n=8
19 tháng 11 2017
a ) Áp dụng công thức n ( n - 1 ) /2
b ) Đề cần cho thêm dư kiện : không có 3 điểm nào thẳng hàng hay có đúng 3 điểm thẳng hàng , ...
Trường hợp này mình làm không có 3 điểm nào thẳng hàng :
Có n( n - 1 ) / 2 = 28
=> n( n - 1 ) = 56
Mà 56 = 8.7
=> n = 8
16 tháng 12 2019
Câu hỏi của Hà Nhật Anh - Toán lớp 6 - Học toán với OnlineMath
CM
11 tháng 6 2017
Đáp án là B
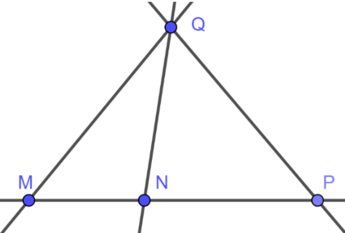
Vì ba điểm M, N, P thẳng hàng nên qua hai điểm bất kì trong ba điểm trên ta đều nhận được một đường thẳng. Vậy từ ba điểm trên ta được một đường thẳng.
Các đường thẳng còn lại là: QM, QN, QP
Vậy có tất cả 4 đường thẳng phân biệt
18 tháng 4 2017
- Vì ba điểm M, N, P thẳng hàng nên qua ba điểm này sẽ có 1 đường thẳng.
- Qua Q và mỗi điểm M, N, P ta sẽ vẽ được 3 đường thẳng là QM, QN, QP.
Vậy ta sẽ vẽ được tất cả 4 đường thẳng là MP, QM, QN, QP.
Ngoài ra, vì đề bài không nhắc đến vị trí của M, N, P nên các bạn cũng có thể vẽ như sau:
Ta có:\(n\left(n-1\right):2=190\)
\(n\left(n-1\right)=380\)
\(n^2-n-380=0\)
\(n^2-20n+19n-380=0\)
\(\left(n+19\right)\left(n-20\right)=0\)
\(n=-19\left(loại\right)\) hoặc \(n=20\left(nhận\right)\)
Vậy \(n=20\)