Cho tam giác vuông vuông tại A có AB bằng 8 cm AC bằng 6 cm trong tam giác ABC cạnh nào có độ dài lớn nhất và bằng bao nhiêu cm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
5 tháng 2 2022
a: BC=10cm
C=AB+BC+AC=6+8+10=24(cm)
b: Xét ΔABD vuông tại A và ΔHBD vuông tại H có
BD chung
\(\widehat{ABD}=\widehat{HBD}\)
Do đó: ΔABD=ΔHBD
c: Ta có: ΔABD=ΔHBD
nên DA=DH
mà DH<DC
nên DA<DC
3 tháng 12 2021
\(BC=\sqrt{AB^2+AC^2}=10\left(cm\right)\\ CM=\dfrac{AC^2}{BC}=3,6\left(cm\right)\\ AM=\dfrac{AB\cdot AC}{BC}=4,8\left(cm\right)\\ \dfrac{BD}{DC}=\dfrac{AB}{AC}=\dfrac{4}{3}\\ \Rightarrow BD=\dfrac{4}{3}DC\\ \text{Mà }BD+DC=BC=10\\ \Rightarrow\dfrac{7}{3}DC=10\\ \Rightarrow DC=\dfrac{30}{7}\left(cm\right)\\ \Rightarrow DM=DC-CM=\dfrac{30}{7}-3,6=\dfrac{24}{35}\left(cm\right)\\ \Rightarrow S_{AMD}=\dfrac{1}{2}AM\cdot DM=\dfrac{1}{2}\cdot\dfrac{24}{35}\cdot4,8=\dfrac{288}{175}\left(cm^2\right)\)
6 tháng 9 2023
ΔABC vuông tại A
=>BC^2=AB^2+AC^2
=>BC^2=6^2+8^2=100
=>BC=10(cm)
Xét ΔBAC có BD là phân giác
nên DA/AB=DC/BC
=>DA/3=DC/5
=>\(\dfrac{DA}{3}=\dfrac{DC}{5}=\dfrac{DA+DC}{3+5}=\dfrac{AC}{8}=1\)
=>DC=5(cm)
KV
6 tháng 9 2023
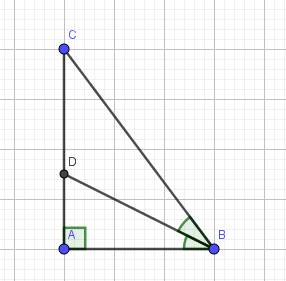
\(\Delta ABC\) vuông tại A
\(\Rightarrow BC^2=AB^2+AC^2\) (Pytago)
\(=6^2+8^2\)
\(=100\)
\(\Rightarrow BC=10\left(cm\right)\)
Do BD là tia phân giác của \(\widehat{ABC}\)
\(\Rightarrow\dfrac{AB}{AD}=\dfrac{BC}{DC}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\dfrac{AB}{AD}=\dfrac{BC}{DC}=\dfrac{AB+BC}{AD+DC}=\dfrac{6+10}{8}=2\)
\(\dfrac{BC}{DC}=2\Rightarrow DC=\dfrac{BC}{2}=\dfrac{10}{2}=5\left(cm\right)\)
26 tháng 3 2021
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Vậy: BC=10cm
HN
8 tháng 5 2022
bài toán vô lí quá nếu mà cân tại A thì AB = AC chứ đáng lẽ ra là vuông tại A chứ:
HN
8 tháng 5 2022
nếu là vuông tại A thì có:
a.Xét tam giác ABC vuông tại A:
BC2=AB2+AC2(định lí pytago)
hay BC2=62+82
BC2=36+64
BC2= \(\sqrt{100}\)
BC=10(cm)
vậy BC=10cm
Xét ΔABC và ΔACM có:
AB=AM(gt)
AC chung
^CAB=^CAM=90o
=>ΔABC=ΔACM(trường hợp gì tự biết) :)
18 tháng 3 2021
a)áp dụng định lý Py-Ta-Go cho ΔABC vuông tại A
ta có:
BC2=AB2+AC2
BC2=62+82
BC2=36+64=100
⇒BC=\(\sqrt{100}\)=10
vậy BC=10
AB và AC không bằng nhau nên không chứng minh được bạn ơi
còn ED và AC cũng không vuông góc nên không chứng minh được luôn
Xin bạn đừng ném đá
CM
5 tháng 12 2018
Diện tích toàn phần là:
S t p = 288 + 2 . 24 = 336 c m 2
Đáp án cần chọn là D
HP
12 tháng 2 2016
xét tg ABC vuông tại A có:
BC2=AB2+AC2
=>BC2=62+82=36+64=100=102
=>BC=10(cm)
trong tam giác ABC vuông tại A thì cạnh huyền BC là cạnh lớn nhất
áp dụng định lý pythagore vào tam giác ABC vuông tại A ta được:
\(BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10\left(cm\right)\)