a,E=5^2022+1/5^2024+1 và F=5^2024+1/5^2026-4 b,M=2^21+3/2^24-6 và N=2^24+3/2^27-6 So sánh giúp mih với a
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NN
13 tháng 2 2023
\(A=\dfrac{2024^{2023}+1}{2024^{2024}+1}\)
\(2024A=\dfrac{2024^{2024}+2024}{2024^{2024}+1}=\dfrac{\left(2024^{2024}+1\right)+2023}{2024^{2024}+1}=\dfrac{2024^{2024}+1}{2024^{2024}+1}+\dfrac{2023}{2024^{2024}+1}=1+\dfrac{2023}{2024^{2024}+1}\)
\(B=\dfrac{2024^{2022}+1}{2024^{2023}+1}\)
\(2024B=\dfrac{2024^{2023}+2024}{2024^{2023}+1}=\dfrac{\left(2024^{2023}+1\right)+2023}{2024^{2023}+1}=\dfrac{2024^{2023}+1}{2024^{2023}+1}+\dfrac{2023}{2024^{2023}+1}=1+\dfrac{2023}{2024^{2023}+1}\)
Vì \(2024>2023=>2024^{2024}>2024^{2023}\)
\(=>2024^{2024}+1>2024^{2023}+1\)
\(=>\dfrac{2023}{2024^{2023}+1}>\dfrac{2023}{2024^{2024}+1}\)
\(=>A< B\)
\(#PaooNqoccc\)
7 tháng 9 2023
1) Ta thấy:
\(4=1+3=1+\sqrt{9}\)
\(1+2\sqrt{2}=1+\sqrt{2^2\cdot2}=1+\sqrt{8}\)
Mà: \(\sqrt{8}< \sqrt{9}\)
\(\Rightarrow1+\sqrt{8}< 1+\sqrt{9}\)
\(\Rightarrow\dfrac{1}{1+\sqrt{8}}>\dfrac{1}{1+\sqrt{9}}\)
\(\Rightarrow\dfrac{1}{1+2\sqrt{2}}>\dfrac{1}{4}\)
2) Ta thấy:
\(2018< 2024\)
\(\Rightarrow\sqrt{2018}< \sqrt{2024}\) (1)
\(2025< 2026\)
\(\Rightarrow\sqrt{2025}< \sqrt{2026}\) (2)
Từ (1) và (2) ta có:
\(\sqrt{2018}+\sqrt{2025}< \sqrt{2024}+\sqrt{2026}\)
HD
So sánh
A = \(\dfrac{2022^{2023}+1}{2022^{2024}+1}\) và B = \(\dfrac{2022^{2022}+1}{2022^{2023}+1}\)
2
4 tháng 7 2023
Trước hết ta phải chứng minh \(\dfrac{a}{b}< \dfrac{a+1}{b+1}\) (a, b ϵ N; a < b).
Thật vậy, \(\dfrac{a}{b}=\dfrac{a\left(b+1\right)}{b\left(b+1\right)}=\dfrac{a+ab}{b^2+b}\) và \(\dfrac{a+1}{b+1}=\dfrac{\left(a+1\right)b}{\left(b+1\right)b}=\dfrac{ab+b}{b^2+b}\).
Mà theo giả thuyết là a < b nên \(\dfrac{a+ab}{b^2+b}< \dfrac{ab+b}{b^2+b}\), suy ra \(\dfrac{a}{b}< \dfrac{a+1}{b+1}\) (a, b ϵ N; a < b).
Từ đây ta có:
\(B=\dfrac{2022^{2022}+1}{2022^{2023}+1}=\dfrac{2022^{2023}+2022}{2022^{2024}+2022}=\dfrac{2022^{2023}+2021+1}{2022^{2024}+2021+1}\)
Đặt \(A_1=\dfrac{2022^{2023}+2}{2022^{2024}+2}=\dfrac{2022^{2023}+1+1}{2022^{2024}+1+1}\), rõ ràng \(A_1>A\).
Đặt \(A_2=\dfrac{2022^{2023}+3}{2022^{2024}+3}=\dfrac{2022^{2023}+2+1}{2022^{2024}+2+1}\), rõ ràng \(A_2>A_1\).
...
Đặt \(A_{2020}=\dfrac{2022^{2023}+2021}{2022^{2024}+2021}=\dfrac{2022^{2023}+2020+1}{2022^{2024}+2020+1}\), rõ ràng \(A_{2020}>A_{2019}\) và \(B>A_{2020}\).
Suy ra \(B>A_{2020}>A_{2019}>...>A_2>A_1>A\). Vậy A < B.
4 tháng 7 2023
Ta có A = \(\dfrac{2022^{2023}}{2022^{2024}}=\dfrac{1}{2022}\) ; B = \(\dfrac{2022^{2022}}{2022^{2023}}=\dfrac{1}{2022}\)
Mà \(\dfrac{1}{2022}=\dfrac{1}{2022}\)
Vậy A = B
21 tháng 7 2023
`a, A = 3020 xx 3110 - 5 = 3020 xx 3109 + 3020 - 5`
`= 3020 xx 3109 + 3015 = B`.
`b, B = (2022-2)(2022+2) = 2022^2-4 < 2022^2 = A.`
KS
7 tháng 10 2021
a) 2021 + 2022 + 2023 + 2024 + 2025 + 2026 + 2027 + 2028 + 2029
= (2021 + 2029) + (2022 + 2028) + (2023 + 2027) + (2024 + 2026) + 2025
= 4050 + 4050 + 4050 + 4050 + 2025
= 4050.4 + 2025
= 16 200 + 2025
= 18 225
KS
7 tháng 10 2021
b)
30.40.50.60 = 3.10.4.10.5.10.6.10 = 3.4.5.6.10000 = 3.20.6.10000 = 3.2.6.10.10000 = 36.100000 = 3600000
TA
3
ND
1
V
2
MH
26 tháng 9 2023
\(A=\dfrac{10^{2024}+1}{10^{2023}+1}=\dfrac{10\left(10^{2023}+1\right)}{10^{2023}+1}-\dfrac{9}{10^{2023}+1}=1-\dfrac{9}{10^{2023}+1}\)
\(B=\dfrac{10^{2023}+1}{10^{2022}+1}=\dfrac{10\left(10^{2022}+1\right)}{10^{2022}+1}-\dfrac{9}{10^{2022}+1}=1-\dfrac{9}{10^{2022}+1}\)
Vì \(\dfrac{9}{10^{2023}+1}< \dfrac{9}{10^{2022}+1}\)
\(\Rightarrow A>B\)
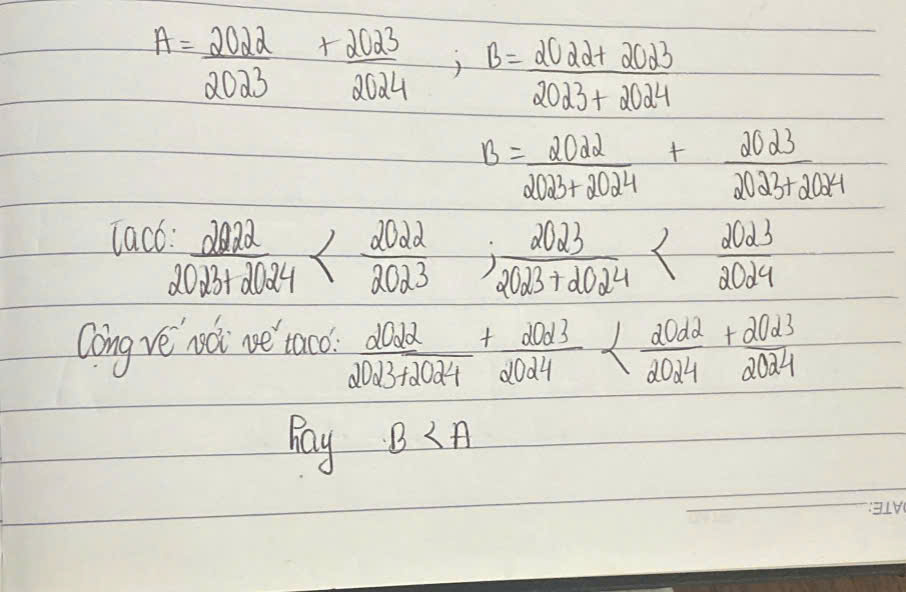
b: \(8M=\dfrac{2^{24}+24}{2^{24}-6}=\dfrac{2^{24}-6+30}{2^{24}-6}=1+\dfrac{30}{2^{24}-6}\)
\(8N=\dfrac{2^{27}+24}{2^{27}-6}=1+\dfrac{30}{2^{27}-6}\)
\(2^{24}-6< 2^{27}-6\)
=>\(\dfrac{30}{2^{24}-6}>\dfrac{30}{2^{27}-6}\)
=>\(\dfrac{30}{2^{24}-6}+1>\dfrac{30}{2^{27}-6}+1\)
=>8M>8N
=>M>N
Để so sánh a và b, trước tiên ta cần tính các giá trị của a, b, M và N. Tính a: a = 5 2022 + 1 5 2024 + 1 a=5 2022 + 5 2024 1 +1 Có thể viết lại: a = 5 2022 + 1 + 1 5 2024 = 5 2022 + 1 + 1 5 2022 ⋅ 5 2 = 5 2022 + 1 + 1 25 ⋅ 5 2022 = 5 2022 + 1 + 1 25 ⋅ 5 2022 a=5 2022 +1+ 5 2024 1 =5 2022 +1+ 5 2022 ⋅5 2 1 =5 2022 +1+ 25⋅5 2022 1 =5 2022 +1+ 25⋅5 2022 1 Tính F: F = 5 2024 + 1 5 2026 − 4 F=5 2024 + 5 2026 1 −4 Có thể viết lại: F = 5 2024 − 4 + 1 5 2026 = 5 2024 − 4 + 1 5 2024 ⋅ 5 2 = 5 2024 − 4 + 1 25 ⋅ 5 2024 F=5 2024 −4+ 5 2026 1 =5 2024 −4+ 5 2024 ⋅5 2 1 =5 2024 −4+ 25⋅5 2024 1 Tính M và N: M = 2 21 + 3 2 24 − 6 M=2 21 + 2 24 3 −6 N = 2 24 + 3 2 27 − 6 N=2 24 + 2 27 3 −6 So sánh a với b, M, N: So sánh giữa a và b cần tính toán và so sánh giá trị cụ thể của các biểu thức trên. Giá trị chính xác của các biểu thức sẽ quyết định mối quan hệ giữa a, b, M và N. Tóm lại, bạn cần tính và so sánh từng giá trị để đưa ra kết luận. Đề bài yêu cầu so sánh a với b, M và N nhưng không có các phép tính cụ thể cho mỗi biểu thức đó. Hãy thực hiện các phép tính để đưa ra so sánh cụ thể hơn.