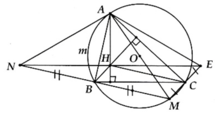
(2,5 điểm) Cho đường tròn $(O; R)$ và một điểm $ A$ sao cho $OA = 2R$, vẽ các tiếp tuyến $AB$, $AC$ với đường tròn $(O; R)$, $B$ và $C$ là các tiếp điểm. Vẽ đường kính $BOD$. Gọi $I$ là giao điểm của đoạn thẳng $OA$ và đường tròn $(O; R)$.
a) Chứng minh bốn điểm $A$, $B$, $O$, $C$ cùng thuộc một đường tròn.
b) Đường trung trực của $BD$ cắt $AC$ và $CD$ lần lượt tại $S$ và $E$. Chứng minh rằng tứ giác $OCEA$ là hình thang cân.
c) $K$ là giao điểm của tia $SI$ và $AB$. Tính theo $R$ diện tích của tứ giác $AKOS$.

a: Xét tứ giác ABOC có \(\widehat{OBA}+\widehat{OCA}=90^0+90^0=180^0\)
nên ABOC là tứ giác nội tiếp
=>A,B,O,C cùng thuộc một đường tròn
b: Xét (O) có
AB,AC là các tiếp tuyến
Do đó: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1),(2) suy ra AO là đường trung trực của BC
=>AO\(\perp\)BC
Xét (O) có
ΔBCD nội tiếp
BD là đường kính
Do đó: ΔBCD vuông tại C
=>BC\(\perp\)CD
mà OA\(\perp\)BC
nên OA//CD
=>OA//CE
Ta có: OE\(\perp\)BD
AB\(\perp\)BD
Do đó: OE//AB
Xét ΔOBA vuông tại B và ΔDOE vuông tại O có
OB=DO
\(\widehat{BOA}=\widehat{ODE}\)(hai góc đồng vị, OA//DE)
Do đó: ΔOBA=ΔODE
=>BA=DE
mà BA=AC
nên DE=AC
Xét tứ giác OAEC có
OA//EC
OE=CA
Do đó: OAEC là hình thang cân