Cho hình tam giác ABC vuông ở A có cạnh AB dài 12cm, cạnh AC dài 15cm. Lấy điểm M nằm trên cạnh AB, điểm N nằm trên cạnh BC sao cho tứ giác MNCA là hình thang. Cho biết đoạn MN dài 10cma. Tính diện tích hình tam giác vuông ABCb. Tính độ dài đoạn MA.c. Tìm tỉ số diện tích của tam giác AMN và tam giác...
Đọc tiếp
Cho hình tam giác ABC vuông ở A có cạnh AB dài 12cm, cạnh AC dài 15cm. Lấy điểm M nằm trên cạnh AB, điểm N nằm trên cạnh BC sao cho tứ giác MNCA là hình thang. Cho biết đoạn MN dài 10cm
a. Tính diện tích hình tam giác vuông ABC
b. Tính độ dài đoạn MA.
c. Tìm tỉ số diện tích của tam giác AMN và tam giác ABC.
diện tích tam giác abc là : 12 nhân 15 chia 2 = 90[cm2]
độ dài đoạn ma là : 10 nhân 12 chia 15 = 8 [cm]
tỉ số đồng dạng : 8/12 = 2/3
tỉ số diện tích : [2/3] nhân 2 = 4/9
diện tích tam giác amn là [4/9] nhân 90 = 40 [cm2]
tỉ số diện tích của 2 tam giác amn và abc là : 40 chia 90 = 4/9
cái dấu "/" là bạn viết theo dạng phân số nhé
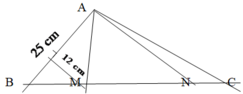
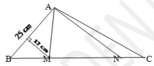
a: ΔABC vuông tại A
=>\(S_{ABC}=\dfrac{1}{2}\times AB\times AC=\dfrac{1}{2}\times12\times15=90\left(cm^2\right)\)
b: Xét ΔBAC có MN//AC
nên \(\dfrac{MN}{AC}=\dfrac{BM}{BA}\)
=>\(\dfrac{10}{15}=\dfrac{BM}{12}\)
=>\(BM=10\cdot\dfrac{12}{15}=12\cdot\dfrac{2}{3}=8\left(cm\right)\)
Ta có: MA+MB=AB
=>MA=AB-BM=12-8=4(cm)
c: Ta có: MN//AC
AC\(\perp\)AB
Do đó: MN\(\perp\)BA tại M
=>ΔMNA vuông tại M
=>\(S_{NMA}=\dfrac{1}{2}\times MN\times MA=\dfrac{1}{2}\times10\times4=20\left(cm^2\right)\)
=>\(\dfrac{S_{AMN}}{S_{ABC}}=\dfrac{20}{90}=\dfrac{2}{9}\)