Cho tam giác ABC, lấy M làm điểm chính giữa BC. a, So sánh diện tích tam giác ABM và diện tích tam giác ACM b, So sánh diện tích tam giác ABM và diện tích tam giác ABC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LT
14 tháng 1 2022
Đáp án:
a) Vì M là trung điểm của BC nên BM bằng CM.
Vì hình tam giác ABM và hình tam giác ACM có chung cạnh AM nên độ dài chiều cao của hình tam giác ABM và ABM bằng nhau.
→→Do có chung độ dài đáy và chiều cao bằng nhau nên diện tích hai hình tam giác bằng nhau.
Vậy diện tích hình tam giác ABM bằng diện tích hình tam giác ACM.
b) Vì BM bằng MC nên BM và MC bằng 1212 BC. Do đó diện tích hình tam giác ABM bằng 1/2 diện tích hình tam giác ABC.
Vậy diện tích hình tam giác ABM bằng 1/2 diện tích hình tam giác ABC.
Ht và tk
Các bạn giải giúp mình với !28 tháng 12 2021
a) Diện tích tam giác ABC là:
\(\text{12 *10 :2= 60 (cm2)}\)
b) Diện tích tam giác AMB là:
\(\text{12 : 2 * 10 :2= 30 (cm^2)}\)
Diện tích tam giác AMC là:
\(\text{12 : 2 *10 :2= 30 (cm^2)}\)
Đáp số: a) 60 cm2
b) Bằng nhau
CM
27 tháng 6 2019
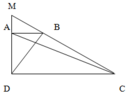
a. S A B C = 1 3 S A D C (Vì cùng chung chiều cao của hình thang ABCD; đáy AB = 1 3 DC)
b. S A B M = S A C M (Vì cùng chung đáy MA, chiều cao AB = 1 3 DC )
c. Theo phần a, ta có: S A B C = S A D C
Mà S A B C D = S A B C + S A D C
Nên S A B C = 1 1 + 3 S A B C D = 1 4 S A B C D
Do đó S A B C D = 64 × 1 4 = 16 ( c m 2 )
Theo phần b, ta có: S A B M = 1 3 S A C M
Mà S A C M = S M A B + S A B C
Nên S M A B = 1 3 - 1 S A B C = 1 2 S A B C
Do đó S M A B = 16 × 1 4 = 8 ( c m 2 )
27 tháng 7 2021
Kẻ đường cao AH
Diện tích tam giác ABM là:
\(S_{ABM}=\dfrac{AH\cdot BM}{2}\)(1)
Diện tích tam giác ACM là:
\(S_{ACM}=\dfrac{AH\cdot CM}{2}\)(2)
Ta có: M là trung điểm của BC(gt)
nên MB=MC(3)
Từ (1), (2) và (3)suy ra \(S_{ABM}=S_{ACM}\)
27 tháng 7 2021
Diện tích ABM = diện tich ACM ( vì có chung đường cao hạ từ A xuống đáy BC và đáy MB = đáy MC )
AH
Akai Haruma
Giáo viên
13 tháng 2 2024
Lời giải:
BM=\frac{1}{2}BC$
$2\times BM=BC$
$2\times BM=BM+MC$
$\Rightarrow BM=MC$
$\Rightarrow \frac{S_{ABM}}{S_{ACM}}=\frac{BM}{CM}=1$
(cùng chiều cao hạ từ điểm A)
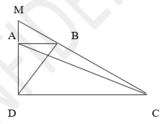
a )Diện tích ABM = ACM b) Diện tích ABM bé gấp đôi diện tích ABC đúng không
a: M là điểm chính giữa của BC
=>M là trung điểm của BC
=>MB=MC
=>\(S_{ABM}=S_{ACM}\)
b: Vì BM<BC
nên \(S_{BMA}< S_{ABC}\)