Bài 3:Cho (d) :y=mx+m-1 và (d'):y=(m-2)x-2m
1)Tìm m để (d) và (d') cắt nhau tại một điểm trên trục tung
2)Tìm m để (d) cắt (d') tại một điểm có hoành độ bằng 2
3)Tìm m để (d) cắt (d') tại A(-1;2)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 5 2021
Câu 1:
a) Ta có: \(x^4+3x^2-4=0\)
\(\Leftrightarrow x^4+4x^2-x^2-4=0\)
\(\Leftrightarrow x^2\left(x^2+4\right)-\left(x^2+4\right)=0\)
\(\Leftrightarrow\left(x^2+4\right)\left(x^2-1\right)=0\)
mà \(x^2+4>0\forall x\)
nên \(x^2-1=0\)
\(\Leftrightarrow x^2=1\)
hay \(x\in\left\{1;-1\right\}\)
Vậy: S={1;-1}
13 tháng 5 2021
Câu 1:
b) Ta có: \(\left\{{}\begin{matrix}x+2y=5\\x-5y=-9\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}7y=14\\x+2y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=2\\x=5-2y=1\end{matrix}\right.\)
Vậy: (x,y)=(1;2)
CM
19 tháng 10 2019
Đáp án D
Gọi M(1+2t;2t;2-t) là giao điểm của d và (Oxy): z =0
Gọi N(1;0;2) là điểm thuộc d. Hình chiếu của N lên (Oxy) là I(1;0;0)
là một véc tơ chỉ phương của d’
DD
Đoàn Đức Hà
Giáo viên
7 tháng 10 2021
Khi tịnh tiến đường thẳng \(\left(d\right)\)thì sẽ thu được đường thẳng song song hoặc trùng với nó nên \(\left(d'\right)\)có dạng
\(2x+y+c=0\).
Lấy \(A\left(0,-3\right)\in\left(d\right)\).
Tịnh tiến điểm \(A\)theo vector \(v\left(1,2\right)\)được \(A'=\left(1,-1\right)\in\left(d'\right)\).
Suy ra \(2.1-1+c=0\Leftrightarrow c=-1\).
Vậy \(\left(d'\right):2x+y-1=0\).
CM
28 tháng 10 2018
Chọn đáp án B
Phương trình đường thẳng d là giao tuyến của hai mặt phẳng (P) và (Oxy) thỏa mãn hệ phương trình:
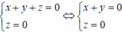
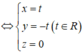
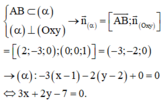
1: Để (d) cắt (d') tại một điểm trên trục tung thì
\(\left\{{}\begin{matrix}a\ne a'\\b=b'\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m\ne m-2\\m-1=-2m\end{matrix}\right.\Leftrightarrow3m=1\)
=>\(m=\dfrac{1}{3}\)
2: Thay x=2 vào y=mx+m-1, ta được:
\(y=m\cdot2+m-1=3m-1\)
Thay x=2 và y=3m-1 vào (d'), ta được:
\(2\left(m-2\right)-2m=3m-1\)
=>3m-1=-4
=>3m=-3
=>m=-1
3: Thay x=-1 và y=2 vào (d), ta được:
\(m\cdot\left(-1\right)+m-1=2\)
=>-m+m-1=2
=>-1=2(vô lý)
vậy: \(m\in\varnothing\)