rút gọn B=\(\frac{1}{a-b}+\frac{1}{a+b}+\frac{2a}{a^2+b^2}+\frac{4a^3}{a^4+b^4}+\frac{8a^7}{a^8+b^8}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, \(\frac{2x+1}{2x^2-5x-3}\)
b, \(\frac{2x+1}{2x^2-5x-3}\)
\(=\frac{2x+1}{2x^2+x-6x-3}\)
\(=\frac{2x+1}{x\left(2x+1\right)-3\left(2x+1\right)}\)
\(=\frac{2x+1}{\left(2x+1\right)\left(x-3\right)}\)
\(=\frac{1}{x-3}\)

D = ( 9 x 2 y 2 – 6 x 2 y 3 ) : ( - 3 x y ) 2 + ( 6 x 2 y + 2 x 4 ) : ( 2 x 2 ) ⇔ D = 9 x 2 y 2 : ( - 3 x y ) 2 – 6 x 2 y 3 : ( - 3 x y ) 2 + 6 x 2 y : ( 2 x 2 ) + 2 x 4 : ( 2 x 2 ) ⇔ D = 1 - 2 3 y + 3 y + x 2 ⇔ D = x 2 + 7 3 y + 1
Đa thức D = x 2 + 7 3 y + 1 có bậc 2
Đáp án cần chọn là: D

Cho mk hỏi muốn rút gọn biểu thức có chứa căn bậc 4 thì làm thế nào nhỉ
Chỉ có cách là bạn phải phân tích số trong biểu thức ra làm căn bậc hai sau đó giải quyết căn 4 thành căn 2
Tùy vào đề bài sẽ có cách làm nha
HT

Chọn B
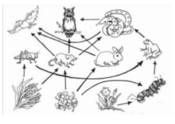
Cách tính: Tính số chuỗi thức ăn với từng sinh vật sản xuất. Ở đây có 3 SVSX.
(1) có tối đa 6 + 8 + 2 = 16 chuỗi thức ăn ⇒ (1) đúng.
(2) có 2 loài ăn thịt đầu bẳng là chim ưng và cú ⇒ (2) sai.
(3) có tối đa 4 + 4 + 2 = 10 chuỗi thức ăn chứa rắn ⇒ (3) sai.
(4) chim ưng thuộc bậc sinh dưỡng cấp 3 và cấp 4 nhưng không thuộc bậc di dưỡng cấp 2. ⇒ (4) sai.
Vậy có 1 ý đúng là (1).

Chọn B
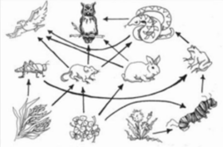
Cách tính: Tính số chuỗi thức ăn với từng sinh vật sản xuất. Ở đây có 3 SVSX.
(1) có tối đa 6 + 8 + 2 = 16 chuỗi thức ăn ⇒ (1) đúng.
(2) có 2 loài ăn thịt đầu bẳng là chim ưng và cú ⇒ (2) sai.
(3) có tối đa 4 + 4 + 2 = 10 chuỗi thức ăn chứa rắn ⇒ (3) sai.
(4) chim ưng thuộc bậc sinh dưỡng cấp 3 và cấp 4 nhưng không thuộc bậc di dưỡng cấp 2. ⇒ (4) sai.
Vậy có 1 ý đúng là (1).

\(=\sqrt{5}-\sqrt{3}+\sqrt{5}-2=2\sqrt{5}-2-\sqrt{3}\)
\(B=\dfrac{1}{a-b}+\dfrac{1}{a+b}+\dfrac{2a}{a^2+b^2}+\dfrac{4a^3}{a^4+b^4}+\dfrac{8a^7}{a^8+b^8}\)
\(=\dfrac{a+b+a-b}{\left(a-b\right)\left(a+b\right)}+\dfrac{2a}{a^2+b^2}+\dfrac{4a^3}{a^4+b^4}+\dfrac{8a^7}{a^8+b^8}\)
\(=\dfrac{2a}{a^2-b^2}+\dfrac{2a}{a^2+b^2}+\dfrac{4a^3}{a^4+b^4}+\dfrac{8a^7}{a^8+b^8}\)
\(=\dfrac{2a\left(a^2+b^2\right)+2a\left(a^2-b^2\right)}{\left(a^2-b^2\right)\left(a^2+b^2\right)}+\dfrac{4a^3}{a^4+b^4}+\dfrac{8a^7}{a^8+b^8}\)
\(=\dfrac{4a^3}{a^4-b^4}+\dfrac{4a^3}{a^4+b^4}+\dfrac{8a^7}{a^8+b^8}\)
\(=\dfrac{4a^3\left(a^4+b^4+a^4-b^4\right)}{\left(a^4-b^4\right)\left(a^4+b^4\right)}+\dfrac{8a^7}{a^8+b^8}\)
\(=\dfrac{8a^7}{a^8-b^8}+\dfrac{8a^7}{a^8+b^8}\)
\(=\dfrac{8a^7\left(a^8-b^8+a^8+b^8\right)}{a^{16}-b^{16}}=\dfrac{16a^{15}}{a^{16}-b^{16}}\)