kẻ hình và giải giúp mình với ( câu a k cm góc nội tiếp nhé )
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a,Xé tứ giác HMBQ có: góc QHP = 90o ( PQ vuông góc với AB tại H )
góc QMB = 90o ( M là hình chiếu của Q trên PB )
=> hai đỉnh H và M nằm kề nhau và cùng nhìn đoạn QB dưới hai gióc bằng nhau ( =90o) => tứ giác HMBQ là tứ giác nội tiếp (đpcm)
ta có tam giác PHM đồng dạng PBQ ( g.g) => \(\frac{HM}{BQ}=\frac{PH}{PB}\Rightarrow\frac{BQ}{PB}=\frac{HM}{PH}=\frac{BQ-HM}{PB-PH}>0\)
mà PB - PH > 0 (do PB > PH)
=> BQ - HM > 0 hay BQ > HM (đpcm)
b, dễ dàng chứng minh được tam giác HKQ đồng dạng với MPQ (g.g)
=> góc MPQ = góc HKQ
mà MPQ = QAH ( hai góc nội tiếp cùng chắn cung QB)
=> góc HKQ = QAH
=> tam giác AQK cân tại Q (đpcm)
Xét tam giác PQB, có:
HB \(\perp\)PQ
QM\(\perp\)PB
Mà QM cắt HB tại K
=> K la trực tâm tam giác PQB
=> PK \(\perp\)QB (t/c trực tâm )
Xét tứ giác PMKH, có
góc PMK = PHK = 90o (QM \(\perp\)PB; BH\(\perp\)PQ)
=> PMK + PHK = 180o
=> tứ giác PMKH nt
=> góc PHM = PKM ( 2 góc nt chắn PB của đtron ngoại tiếp tg PMKH )
Vì tứ giác HMBQ nội tiếp ( cmt)
=> MBQ + QHM = 180o ( t/c tg nt )
ma PHM + MHQ = 180o ( kề bù )
=> MBQ = PHM
mà PHM = PKM ( cmt )
=> MBQ = PKM
Xét tam giác PKM và PBI, có
MBQ = PKM ( cmt )
IPB chung
=> tam giác PKM đồng dạng tam giác PBI (g.g)
=> PIB = PMK = 90o
=> PI \(\perp\)IB
hay PI\(\perp\)QB
mà PK \(\perp\)QB ( cmt )
=> PI \(\equiv\)PK
=> P, I, K thẳng hàng

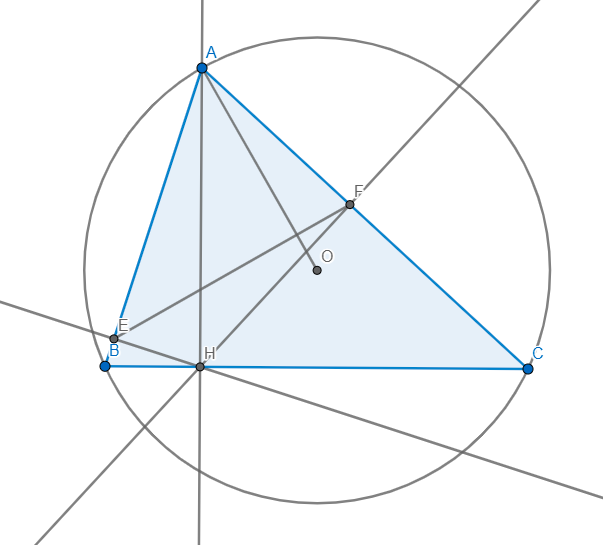
a) Ta có: \(\angle AEH+\angle AFH=90+90=180\Rightarrow AEHF\) nội tiếp
b) AEHF nội tiếp \(\Rightarrow\angle EFA=\angle EHA=90-\angle BHE=\angle ABC\)
c) Ta có: \(\angle OAC=\dfrac{180-\angle AOC}{2}=90-\dfrac{1}{2}\angle AOC=90-\angle ABC\)
\(\Rightarrow\angle OAC+\angle ABC=90\Rightarrow\angle OAC+\angle AFE=90\Rightarrow OA\bot EF\)

a: Xét tứ giác AHMK có
\(\widehat{AHM}=\widehat{AKM}=\widehat{KAH}=90^0\)
Do đó; AHMK là hình chữ nhật

đầu bài sai Quá K bn nhé
a, bỏ qua
b,bn tự vẽ hình nhé
Xét tam giác vuông BAK và tam giác vuông BEK co :
góc ABK = goc EBK ( VI BK LA PHAN GIAC )
BK CHUNG
=> TAM GIÁC VUÔNG BAK = TẢM GIÁC VUÔNG BEK ( CẠNH HUYỀN GÓC NHỌN )
DO ĐÓ : AK = KE ( 2 CẠNH TƯƠNG ỨNG )
Xét tam giác vuông AKF và tam giac vuong ECK co :
GÓC AKF = GÓC EKC ( HAI GÓC ĐỐI ĐỈNH )
AK=EK ( CMT )
=> TAM GIÁC VUÔNG AKF = TAM GIÁC VUÔNG BEK ( CẠNH GÓC VUÔNG VÀ GÓC NHỌN KỀ CẠNH ẤY )
DO ĐÓ KF = KC ( 2 CẠNH TƯƠNG ỨNG )
c, VÌ FC VUÔNG GÓC VỚI AC ; CA VUÔNG GÓC VỚI BA VÀ FC CẮT CA TẠI K
=> K LÀ GIAO ĐIỂM CỦA BA ĐƯỜNG CAO TRONG TAM GIÁC BFC ( T/C BA ĐG CAO TRONG TAM GIÁC )
DO ĐÓ BK CŨNG VUÔNG GÓC VỚI FC
[ XONG RỒI BN ƠI ]
a: Xét (D) có
ΔBEC nội tiếp
BC là đường kính
Do đó: ΔBEC vuông tại E
=>CE\(\perp\)AB tại E
Xét (D) có
ΔBFC nội tiếp
BC là đường kính
Do đó: ΔBFC vuông tại F
=>BF\(\perp\)AC tại F
Xét tứ giác AEGF có \(\widehat{AEG}+\widehat{AFG}=90^0+90^0=180^0\)
nên AEGF là tứ giác nội tiếp
=>A,E,G,F cùng thuộc một đường tròn
b: Xét (D) có
ΔBIC nội tiếp
BC là đường kính
Do đó: ΔBIC vuông tại I
Xét ΔIBC vuông tại I có IH là đường cao
nên \(BH\cdot BC=BI^2\)
c: Vì B,E,F,C cùng thuộc (D)
nên BEFC là tứ giác nội tiếp
=>\(\widehat{BEF}+\widehat{BCF}=180^0\)
mà \(\widehat{BEF}+\widehat{AEF}=180^0\)(hai góc kề bù)
nên \(\widehat{AEF}=\widehat{ACB}\)
Xét ΔAEC vuông tại E có \(cosEAC=\dfrac{AE}{AC}\)
=>\(\dfrac{AE}{AC}=cos60=\dfrac{1}{2}\)
Xét ΔAEF và ΔACB có
\(\widehat{AEF}=\widehat{ACB}\)
\(\widehat{EAF}\) chung
Do đó: ΔAEF~ΔACB
=>\(\dfrac{EF}{CB}=\dfrac{AE}{AC}\)
=>\(\dfrac{EF}{6}=\dfrac{1}{2}\)
=>EF=3(cm)
a) Chứng minh BEC = BFC = 90° ; Từ đó suy ra 4 điểm A, E, G, F cùng thuộc một đường tròn.
Chứng minh BEC = BFC = 90°:
Vì BC là đường kính của đường tròn tâm D, nên E và F là hai điểm nằm trên đường tròn.
Theo tính chất của góc nội tiếp chắn nửa đường tròn, ta có:
∠BEC = ∠BFC = 90°
Suy ra 4 điểm A, E, G, F cùng thuộc một đường tròn:
Xét tứ giác AEGF có:
∠AEG = 90° (do ∠BEC = 90°)
∠AFG = 90° (do ∠BFC = 90°)
Tứ giác AEGF có hai góc đối nhau vuông, nên AEGF là tứ giác nội tiếp.
Vậy 4 điểm A, E, G, F cùng thuộc một đường tròn.
b) Gọi I là giao điểm của (D) và AH (I nằm giữa A và G). Chứng minh BI² = BH.BC
Xét △BIC có BI là đường cao, ta có:
BI² = BH.BC (hệ thức lượng trong tam giác vuông)
c) Trong trường hợp BAC = 60° và BC = 6cm. Tính bán kính của đường tròn ngoại tiếp ∆AEF.
Tính BC:
Vì △ABC có ∠BAC = 60° và AB = AC, nên △ABC là tam giác đều. ⇒ AB = AC = BC = 6cm
Tính AE và AF:
Vì E và F lần lượt là hình chiếu của B và C trên AB và AC, nên AE và AF lần lượt là đường cao của △ABC.
Trong tam giác đều, đường cao cũng là đường trung tuyến, nên AE = AF = (1/2)AB = (1/2)AC = 3cm
Tính bán kính đường tròn ngoại tiếp △AEF:
Gọi R là bán kính đường tròn ngoại tiếp △AEF.
Theo công thức bán kính đường tròn ngoại tiếp tam giác, ta có: R = (AE.AF.EF) / (4.S△AEF)
Trong đó: EF = BC = 6cm (do AEGF là hình chữ nhật)
S△AEF = (1/2).AE.AF.sin∠EAF = (1/2).3.3.sin60° = (9√3)/4 cm²
Thay số vào công thức, ta được:
R = (3.3.6) / (4.(9√3)/4) = 2√3 cm
Kết luận:
Bán kính của đường tròn ngoại tiếp △AEF là 2√3 cm.