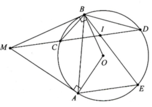
(2,5 điểm) Cho đường tròn $(O;\,R)$ và đường thẳng $d$ không có điểm chung với đường tròn $(O)$. Gọi $H$ là hình chiếu của $O$ trên đường thẳng $d$. Từ một điểm $M$ bất kì trên đường thẳng $d,\,( M \ne H )$, kẻ hai tiếp tuyến $MA$, $MB$ với đường tròn $(O)$, ($A$ và $B$ là các tiếp điểm). Dây $AB$ cắt $OH$ tại $C$ và cắt $OM$ tại $D$. Chứng minh rằng:
a) Tứ giác $MAOB$ nội tiếp.
b) $OC.OH=OD.OM$.
c) Khi điểm $M$ di chuyển trên đường thẳng $d$ thì dây $AB$ luôn đi qua một điểm cố định.


a: Xét tứ giác MAOB có \(\widehat{MAO}+\widehat{MBO}=90^0+90^0=180^0\)
nên MAOB là tứ giác nội tiếp
b: Xét (O) có
MA,MB là các tiếp tuyến
Do đó: MA=MB
=>M nằm trên đường trung trực của AB(1)
ta có: OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1),(2) suy ra MO là đường trung trực của AB
=>MO\(\perp\)AB tại D
Xét ΔODC vuông tại D và ΔOHM vuông tại H có
\(\widehat{DOC}\) chung
Do đó: ΔODC~ΔOHM
=>\(\dfrac{OD}{OH}=\dfrac{OC}{OM}\)
=>\(OD\cdot OM=OC\cdot OH\)