hai tam giác đồng dang
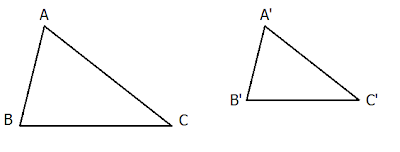
Tam giác đồng dạng có hai tính chất quan trọng sau đây:
∠A=∠A′, ∠B=∠B′, ∠C=∠C′
Ba cặp cạnh tỉ lệ với nhau
ABA′B′=BCB′C′=CAC′A′
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 2 2019
- Có
- Các trường hợp là :
đồng dạng (c.c.c) , đồng dạng (g.g) , đông dạng (c.g.c)
Tam giác đồng dạng có hai tính chất quan trọng sau đây:
Ba cặp cạnh tỉ lệ với nhau
4 tháng 2 2019
đồng dạng (c.c.c) , đồng dạng (g.g) , đồng dạng (c.g.c)
Tam giác đồng dạng có hai tính chất quan trọng sau đây:
∠A=∠A′, ∠B=∠B′, ∠C=∠C′
Ba cặp cạnh tỉ lệ với nhau
ABA′B′=BCB′C′=CAC′A′
Vậy làm thế nào để chứng minh hai tam giác là đồng dạng với nhau. Thông thường chúng ta có ba cách sau đây.
Trường hợp Góc - Góc: hai tam giác có hai cặp góc bằng nhau là hai tam giác đồng dạng với nhau
Ở hình dưới đây, nếu chúng ta chỉ ra được
∠A=∠A′ và ∠B=∠B′
thì chúng ta có thể kết luận rằng hai tam giác ABC và A′B′C′ là đồng dạng với nhau.
Trường hợp Cạnh - Cạnh - Cạnh: hai tam giác có ba cặp cạnh tỉ lệ với nhau là hai tam giác đồng dạng với nhau
Ở hình dưới đây, nếu chúng ta chỉ ra được
ABA′B′=BCB′C′=CAC′A′
thì chúng ta có thể kết luận rằng hai tam giác ABC và A′B′C′ là đồng dạng với nhau.
Trường hợp Cạnh - Góc - Cạnh: hai tam giác có hai cặp cạnh tỉ lệ với nhau và cặp góc xen giữa hai cặp cạnh này bằng nhau thì đó là hai tam giác đồng dạng với nhau
Ở hình dưới đây, nếu chúng ta chỉ ra được
ABA′B′= BCB′C′ và ∠B=∠B′
thì chúng ta có thể kết luận rằng hai tam giác ABC và A′B′C′ là đồng dạng với nhau.
- Nếu hai tam giác là hai tam giác vuông thì việc chứng minh hai tam giác là đồng dạng còn đơn giản hơn nữa. Chúng ta có các cách sau đây.
Trường hợp Góc Nhọn: hai tam giác vuông có một cặp góc nhọn bằng nhau là hai tam giác đồng dạng với nhau
Ở hình dưới đây, nếu chúng ta chỉ ra được
∠A=∠A′
thì chúng ta có thể kết luận rằng hai tam giác vuông ABC và A′B′C′ là đồng dạng với nhau.
Trường hợp Cạnh - Cạnh: hai tam giác vuông có hai cặp cạnh tỉ lệ với nhau là hai tam giác đồng dạng với nhau
Ở hình trên đây, nếu chúng ta chỉ ra được
ABA′B′= BCB′C′, hoặc BCB′C′= CAC′A′, hoặc CAC′A′= ABA′B′
thì chúng ta có thể kết luận rằng hai tam giác vuông ABC và A′B′C′ là đồng dạng với nhau.
4 tháng 5 2019
Bạn tự vẽ hình nhé :^
a) Xét tam giác ABD và tam giác ACE có :
góc ADB = góc ACE ( vì cùng bằng 90 độ )
góc BAC chung
=> tam giác ABD đồng dạng với tam giác ACE ( g.g)
b) Vì tam giác ABD đồng dạng với tam giác ACE (cmt)
=> \(\frac{AB}{AC}=\frac{AD}{AE}\)( định nghĩa tam giác đồng dạng)
Xét tam giác ADE và tam giác ABC có
\(\frac{AD}{AE}=\frac{AB}{AC}\)(cmt)
\(\widehat{BAC}\)chung
\(\Rightarrow\) tam giác ADE đồng dạng với tam giác ABC ( c.g.c)
Còn câu c là gì vậy ạ ?
23 tháng 1 2024
a: Xét ΔAMN và ΔACB có
\(\widehat{AMN}=\widehat{ACB}\)
\(\widehat{MAN}\) chung
Do đó: ΔAMN~ΔACB
b: Ta có: ΔAMN~ΔACB
=>\(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)
=>\(\dfrac{AM}{AN}=\dfrac{AC}{AB}\)
Xét ΔAMC và ΔANB có
\(\dfrac{AM}{AN}=\dfrac{AC}{AB}\)
\(\widehat{MAC}\) chung
Do đó: ΔAMC~ΔANB
c: Sửa đề: Gọi O là giao điểm của BN với CM
Ta có: ΔABN~ΔACM
=>\(\widehat{ABN}=\widehat{ACM}\)
Xét ΔOBM và ΔOCN có
\(\widehat{OBM}=\widehat{OCN}\)
\(\widehat{BOM}=\widehat{CON}\)(hai góc đối đỉnh)
Do đó: ΔOBM~ΔOCN
=>\(\dfrac{OB}{OC}=\dfrac{OM}{ON}\)
=>\(\dfrac{OB}{OM}=\dfrac{OC}{ON}\)
Xét ΔOBC và ΔOMN có
\(\dfrac{OB}{OM}=\dfrac{OC}{ON}\)
\(\widehat{BOC}=\widehat{MON}\)(hai góc đối đỉnh)
Do đó: ΔOBC~ΔOMN
HH
19 tháng 3 2020
A B C D E A' B' C'
+ Dựng ΔADE 
ΔABC theo tỉ số 2/3
Trên AB lấy D, trên AC lấy E sao cho \(AD=\frac{2}{3}AB;AE=\frac{2}{3}AC\)
Suy ra : \(\frac{AD}{AB}=\frac{AE}{AC}=\frac{2}{3}\)
Khi đó theo định lý Ta-let đảo ta suy ra DE // BC
⇒ ΔADE ΔABC theo tỉ số 2/3.
+ Dựng ΔA’B’C’ = ΔADE
Vẽ đoạn A’B’ = AD.
Dựng góc \(\widehat{A'B'x}=\widehat{ADE}\)
Trên tia B’x lấy điểm C’ sao cho B’C’ = DE.
Nối C’A’ ta được ΔA’B’C’ = ΔADE (c.g.c)
Suy ra: ΔA’B’C’ đồng dạng với ΔADE theo tỉ số:
\(k_1=\frac{A'B'}{AD}=1\)
Mà tam giác ADE tam giác ABC theo tỉ số
\(k_2=\frac{AD}{AB}=\frac{2}{3}\)
=> Tam giác A'B'C' tam giác ABC theo tỉ số
\(k=k_1.k_2=\frac{A'B'}{AB}=\frac{2}{3}\)
24 tháng 1 2022
a) Xét tam giác HMN và tam giác MNP:
Góc B chung.
Góc MHN = Góc NMP (cùng = 90o).
=> Tam giác HMN \(\sim\) Tam giác MNP (g - g).
b) Xét tam giác MNP vuông tại M, MH là đường cao:
=> MH2 = NH . PH (Hệ thức lượng trong tam giác vuông).
c) Xét tam giác NFH và tam giác MEH:
Góc FNH = Góc EMH (cùng phụ với góc MPN).
Góc NHF = Góc MHE (cùng phụ với góc MHF).
=> Tam giác NFH \(\sim\) Tam giác MEH (g - g).
24 tháng 1 2022
a: Xét ΔHNM vuông tại H và ΔMNP vuông tại M có
\(\widehat{N}\) chung
Do đó: ΔHNM\(\sim\)ΔMNP
b: Xét ΔMNP vuông tại M có MH là đường cao
nên \(MH^2=NH\cdot PH\)
12 tháng 5 2023
a: CB=10cm
BD là phân giác
=>AD/AB=CD/BC
=>AD/3=CD/5=8/8=1
=>AD=3cm; CD=5cm
b: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạng với ΔHBA
=>BA^2=BH*BC
c: Xét ΔBAD vuông tại A và ΔBHI vuông tại H có
góc ABD=góc HBI
=>ΔBAD đồng dạng với ΔBHI
=>BA/BH=BD/BI
=>BA/BD=BH/BI
=>BA/BH=BD/BI=BC/BA
=>ΔBDC đồng dạng với ΔBIA
NB
3 tháng 5 2023
a)Có tg ABC vuông tại a
áp dụng đl pytago ta có:
\(BC^2=AB^2+AC^2=6^2+8^2=100\\ \Rightarrow BC=10\left(cm\right)\)
Có BD là đg phân giác tg ABC
\(\Rightarrow\dfrac{AD}{DC}=\dfrac{AB}{BC}=\dfrac{6}{10}=\dfrac{3}{5}\left(1\right)\)
lai co: AD+DC=AC=8
=>AD=8-DC
thay vao 1
\(\Rightarrow\dfrac{8-DC}{DC}=\dfrac{3}{5}\)
\(\Leftrightarrow DC=5\\ \Rightarrow AD=3\)
b) xét tg ABC và tg HBA có:
+góc BAH = AHB(=90 độ)
+góc B chung
=> tg ABC đồng dạng tg HBA (gg) (đpcm)
\(\Rightarrow\dfrac{AB}{HB}=\dfrac{BC}{BA}\\ \Leftrightarrow AB^2=HB.BC\left(dpcm\right)\)
c) có: + góc C =\(90^o-\widehat{B}\) (goc A = 90 do)
+ \(\widehat{BAH}=90^o-\widehat{B}\) (goc AHB =90do)
=> goc BAH = goc C
xet tg ABI va tg CBD co
+goc BAH =goc C
+ goc ABI = goc DBC (BD la phan giac)
=> tg ABI va tg CBD dong dang (g.g) (dpcm)
25 tháng 3 2017
a, Xét tgiác ABH và tgiác CBA có
Góc AHB = BAC (=900)
Góc B chung
==> ABH đồng dạng CBA (g-g)
tương tự cminh tgiác ACH đồng dạng BCA(g-g)
vì ABH đồng dạng CBA, ACH đồng dạng BCA ==>ABH đồng dạng CAH (bc)
b, xét tam giác AHB và tam giác HPQ có
góc H chung
HP/HB = HQ/HA (=1/2)
==> tam giác AHB đồng dạng QHP
==> AH/HQ = HB/HP
==> AH.HP=HB.HQ
C, Sai đề rồi bạn ơi
Nếu một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.
Nếu một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng giạng với tam giác đã cho