
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xét cặp tam giác thứ nhất: Hình a và Hình c.
Ta có: \(\frac{3}{9} = \frac{1}{3};\frac{7}{{21}} = \frac{1}{3};\frac{{8\frac{1}{3}}}{{25}} = \frac{1}{3}\).
Do đó, tam giác ở Hình a và Hình c đồng dạng với nhau.
Xét cặp tam giác thứ hai: Hình b và Hình d.
Ta có: \(\frac{7}{{14}} = \frac{1}{2};\frac{7}{{14}} = \frac{1}{2};\frac{3}{6} = \frac{1}{2}\).
Do đó, tam giác ở Hình b và Hình d đồng dạng với nhau.

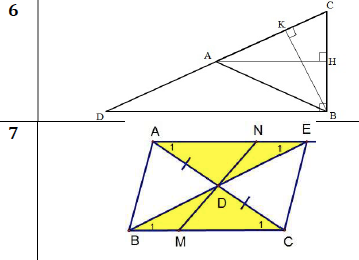
Câu 6:
\(\left\{{}\begin{matrix}\widehat{ACB}\text{ chung}\\\widehat{CKB}=\widehat{CHA}=90^0\end{matrix}\right.\Rightarrow\Delta CHA\sim\Delta CKB\left(g.g\right)\\ \left\{{}\begin{matrix}\widehat{ACB}\text{ chung}\\\widehat{AHC}=\widehat{DBC}=90^0\end{matrix}\right.\Rightarrow\Delta CHA\sim\Delta CBD\left(g.g\right)\\ \left\{{}\begin{matrix}\widehat{ACB}\text{ chung}\\\widehat{CKB}=\widehat{DBA}=90^0\end{matrix}\right.\Rightarrow\Delta CKB\sim\Delta CBD\left(g.g\right)\\ \Delta CHA\sim\Delta CKB\Rightarrow\dfrac{CH}{CK}=\dfrac{CA}{CB}\Rightarrow\Delta CKH\sim\Delta CBA\left(c.g.c\right)\)

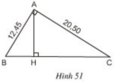
Trong hình bên có 3 cặp tam giác đồng dạng là BHA và BAC; CHA và CAB; HAB và HCA.

Ta có:
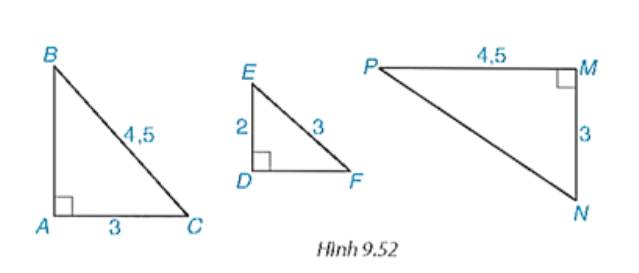
AC/BC = 3/4,5 = 2/3
DE/EF = 2/3
⇒ AC/BC = DE/EF
∆ABC và ∆DFE có:
AC/BC = DE/EF = 2/3
∠BAC = ∠EDF = 90⁰
⇒ ∆ABC ∽ ∆DFE (cạnh huyền - cạnh góc vuông)
Tam giác ABC và tam giác DEF có:
\( \widehat A = \widehat D = 90^0 \)
\( \frac {AC}{DE} = \frac {BC}{EF} = \frac {3}{2} \)
\( \Rightarrow \Delta ABC \backsim \Delta DFE (ch - cgv) \)

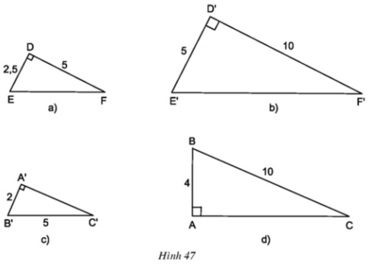
+ΔDEF vuông tại D và ΔD'E'F' vuông tại D’ có:
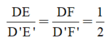
⇒ ΔDEF ∼ ΔD'E'F' (hai cạnh góc vuông)
*)Áp dụng định lí py ta go vào tam giác A’B’C’ vuông tại A’ có:
A’C’2 + A’B’2 = B’C’2
=> A’C’2 + 22 = 52
Suy ra: A’C’2 = 25 – 4 = 21 nên 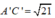
*)Áp dụng định lí py ta go vào tam giác ABC vuông tại A có:
AB2 + AC2 = BC2
Thay số: 42 + AC2 = 102
Suy ra: AC2 = 100 – 16 = 84 nên

Do đó, ∆ A’B’C’ đồng dạng với tam giác ABC ( trường hợp 2).

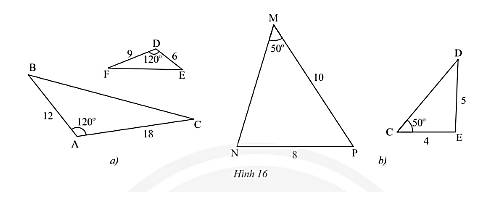
- Xét Hình 16a
Ta có: \(\frac{{DE}}{{AB}} = \frac{6}{{12}} = \frac{1}{2};\frac{{DF}}{{AC}} = \frac{9}{{18}} = \frac{1}{2}\)
Xét tam giác \(DEF\) và tam giác \(ABC\) ta có:
\(\frac{{DE}}{{AB}} = \frac{{DF}}{{AC}} = \frac{1}{2}\)
\(\widehat {BAC} = \widehat {EDF} = 120^\circ \)
Do đó, \(\Delta DEF\backsim\Delta ABC\) (c.g.g)
- Xét Hình 16b
Ta có: \(\frac{{CE}}{{NP}} = \frac{4}{8} = \frac{1}{2};\frac{{DE}}{{MP}} = \frac{5}{{10}} = \frac{1}{2}\)
Tuy nhiên, quan sát hình vẽ ta có thể thấy góc tạo bởi cạnh \(MP;NP\) là \(\widehat P\) và góc tạo bởi cạnh \(DE;CE\) là góc \(\widehat E\).
Ta thấy hai góc này không bằng nhau nên chúng không đồng dạng.

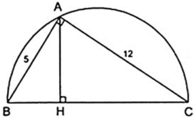
a) ΔABC  ΔHBA vì Â = Ĥ = 90º, B̂ chung
ΔHBA vì Â = Ĥ = 90º, B̂ chung
ΔABC  ΔHAC vì Â = Ĥ = 90º, Ĉ chung
ΔHAC vì Â = Ĥ = 90º, Ĉ chung
ΔHBA 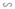 ΔHAC vì cùng đồng dạng với ΔABC.
ΔHAC vì cùng đồng dạng với ΔABC.
b) + ΔABC vuông tại A
⇒ BC2 = AB2 + AC2
(Theo định lý Pytago)


Xét ΔPED và ΔPMN có
\(\dfrac{PE}{PM}=\dfrac{PD}{PN}=\dfrac{1}{2}\)
\(\widehat{P}\) chung
Do đó: ΔPED~ΔPMN
=>\(k=\dfrac{PE}{PM}=\dfrac{1}{2}\)
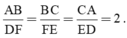
Xét ΔABC và ΔPNM có
\(\dfrac{AB}{PN}=\dfrac{BC}{NM}=\dfrac{AC}{PM}\left(\dfrac{3}{4,5}=\dfrac{6}{9}=\dfrac{5}{7,5}=\dfrac{2}{3}\right)\)
=>ΔABC~ΔPNM