Ta có chữ số a, b và biết 9a+8b⋮9. Chứng minh 2a+4b⋮9.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a; CM (2a + 6) ⋮ 2
Ta có: 2a + 6 = 2.(a + 3) ⋮ 2 \(\forall\) a(đpcm)
b; (9a + 27b) ⋮ 9
Ta có: 9a + 27b = 9(a + 3b) ⋮ 9 \(\forall\) a; b
c; CM : (2a + 4b + 1) không chia hết cho 2
Ta có: 2a +4b + 1 = 2(a + 2b) + 1
Vì 2.(a + 2b) ⋮ 2 mà 1 không chia hết cho 2 nên
(2a + 4b + 1) không chia hết cho 2 (đpcm)
d; CM : (5a + 15b + 3) không chia hết cho 5
Ta có: 5a + 15b + 3 = (5a+ 15b) + 3 = 5.(a + 3b) + 3
Vì 5.(a + 3b) ⋮ 5 mà 3 không chia hết cho 5 nên
(5a + 15b + 3) không chia hết cho 5 (đpcm)


a+5b chia hết cho 9 nên suy ra: a chia hết cho 9 và 5b cũng chia hết cho 9
Vì 5b chia hết cho 9 nên b chắc chắn phải chia hết cho 9. Ta có:
a chia hết cho 9 suy ra 2a chia hết cho 9.
b chia hết cho 9 suy ra 4b chia hết cho 9.
2 số đều chia hết cho 9 thì suy ra hiệu của chũng cũng chia hết cho 9.
Vậy 2a-4b chia hết cho 9.

a)
`a<b`
`<=>3a<3b`
`<=>3a-5<3b-5`
b)
`a<b`
`<=>-8a> -8b`
`<=>-8a-3> -8b-3`
c)
`a<b`
`<=>4a<4b`
`<=>4a+9<4b+9`
mà `4a-7<4a+9`
`<=>4a-7<4b+9`



Lời giải:
Một số tự nhiên có cùng số dư khi chia cho 9 với tổng các chữ số của nó. Tức là:
$a-S(a)\vdots 9$
$2a-S(2a)\vdots 9$
$\Rightarrow a-k\vdots 9; 2a-k\vdots 9$
$\Rightarrow (2a-k)-(a-k)\vdots 9$
$\Rightarrow a\vdots 9$
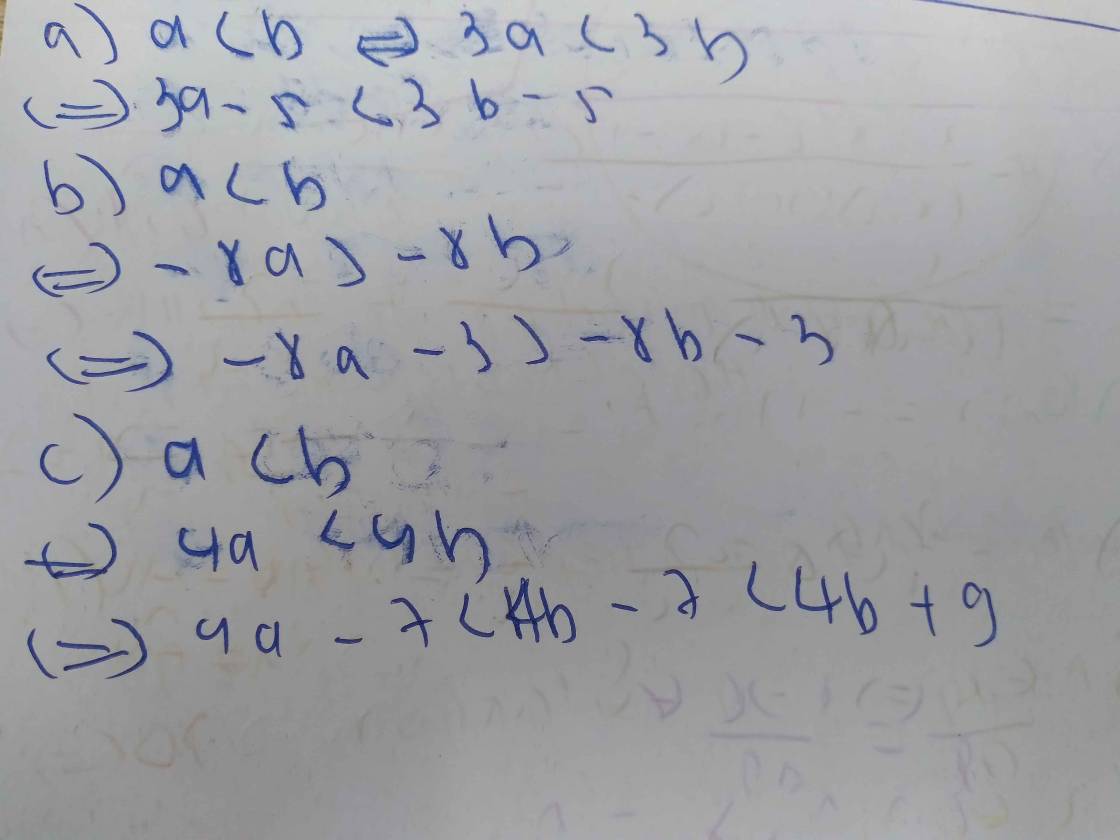
9a⋮9 và 2a⋮9 vậy aϵ BC(9,2)={0;18;36;...}
8b⋮9 và 4b⋮9 vậy bϵ BC(8,4)={0;24;48;72;...}
mà BC(8,4) ⋮9 nên => bϵ{0;72;...}
Chắc z :))