tìm x nguyên sao cho giá trị biểu thức 3x2 -5x-7 chia hết cho giá trị biêu thức x-3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


>_ là lớn hơn hoặc bằng nha do bị lỗi chính tả
_< là bé hơn hoặc bằng
A,
2-5x >_ 3(2-x)
⇔ 2-5x >_ 6-3x
⇔ -5x+3x >_ 6-2
⇔ -2x >_ 3
⇔ x _< \(\dfrac{-3}{2}\)
Tập nghiệm { x / x _< \(\dfrac{-3}{2}\)}
B,
-4x + 3 _< 5x - 7
⇔ -4x - 5x _< -7 - 3
⇔ -9x _< -10
⇔ x >_ \(\dfrac{10}{9}\)
Tập nghiệm { x / x >_ \(\dfrac{10}{9}\) }

Bài 3:
Ta có: \(2n^2+n-7⋮n-2\)
\(\Leftrightarrow2n^2-4n+5n-10+3⋮n-2\)
\(\Leftrightarrow n-2\in\left\{1;-1;3;-3\right\}\)
hay \(n\in\left\{3;1;5;-1\right\}\)

b: \(\Leftrightarrow3n^3+n^2+9n^2+3n-3n-1-4⋮3n+1\)
\(\Leftrightarrow3n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
\(\Leftrightarrow n\in\left\{0;-1;1\right\}\)

a) Cho x2 - x + 5=0 =>x={ \(\frac{1}{2}+\frac{\sqrt{19}}{2}i;\frac{1}{2}-\frac{\sqrt{19}}{2}i\) }
Thay giá trị của x là \(\frac{1}{2}+\frac{\sqrt{19}}{2}i\)hoặc \(\frac{1}{2}-\frac{\sqrt{19}}{2}i\) vừa tìm được vào x4 - x3 + 6x2- x sẽ luôn được kết quả là -5
=>-5 +a=0 => a=5
b) Cho x+2=0 => x=-2
Thay giá trị của x vào biểu thức 2x3 - 3x2 + x sẽ được kết quả là -30
=> -30 + a=0 => a=30
a) Cho 3n +1 =0 => n= \(\frac{-1}{3}\)
Thay n= \(\frac{-1}{3}\)vào biểu thức 3n3 + 10n2 -5 sẽ được kết quả -4
Vậy n = -4
b) Cho n-1=0 => n=1
Thay n=1 vào biểu thức 10n2 + n -10 sẽ được kết quả là 1
Vậy n = 1

a: \(\dfrac{A}{B}=\dfrac{x^3+x^2+2x^2+2x+x+1-3}{x+1}=x^2+2x+1-\dfrac{3}{x+1}\)
b: Để A chia hết cho B thì \(x+1\in\left\{1;-1;3;-3\right\}\)
=>\(x\in\left\{0;-2;2;-4\right\}\)

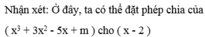
để tìm số dư, rồi cho số dư đó bằng 0, từ đó tìm được giá trị của m.
Mở rộng: Bài toán này ta áp dụng phân tích đa thức thành nhân tử để giải toán

Ta có:
3x2-5x-7=3x2-9x+4x-12+5=3x(x-3)+4(x-3)+5=(x-3)(3x+4)+5
Nhận thấy: (x-3)(3x+4) luôn chia hết cho x-3 với mọi x
=> Để biểu thức nguyên thì 5 phải chia hết cho x-3
=> x-3 là ước của 5 => x-3=(-5,-1,1,5)
=> x thuộc (-2; 2; 4; 8)