từ điểm A nằm ngoài đường tròn (O;R) sao cho OA=2R, vẽ hai tiếp tuyến AB, AC đến đường tròn (O)(B,C là tiếp điểm). Gọi H là giao điểm của OA và BC. Vẽ đường kính BD của đường tròn (O). a,Chứng minh: AO vuông góc BC và AO song song CD b,Chứng minh: 4OH * OA = BD2 c,Gọi N là giao điểm của AD và đường tròn (O). Chứng minh: AN * AD = AH * AO d, Kẻ CK vuông góc BD tại K, I là giao điểm của CK và AD. Chứng...
Đọc tiếp
từ điểm A nằm ngoài đường tròn (O;R) sao cho OA=2R, vẽ hai tiếp tuyến AB, AC đến đường tròn (O)(B,C là tiếp điểm). Gọi H là giao điểm của OA và BC. Vẽ đường kính BD của đường tròn (O). a,Chứng minh: AO vuông góc BC và AO song song CD b,Chứng minh: 4OH * OA = BD2 c,Gọi N là giao điểm của AD và đường tròn (O). Chứng minh: AN * AD = AH * AO d, Kẻ CK vuông góc BD tại K, I là giao điểm của CK và AD. Chứng minh: IC = IK
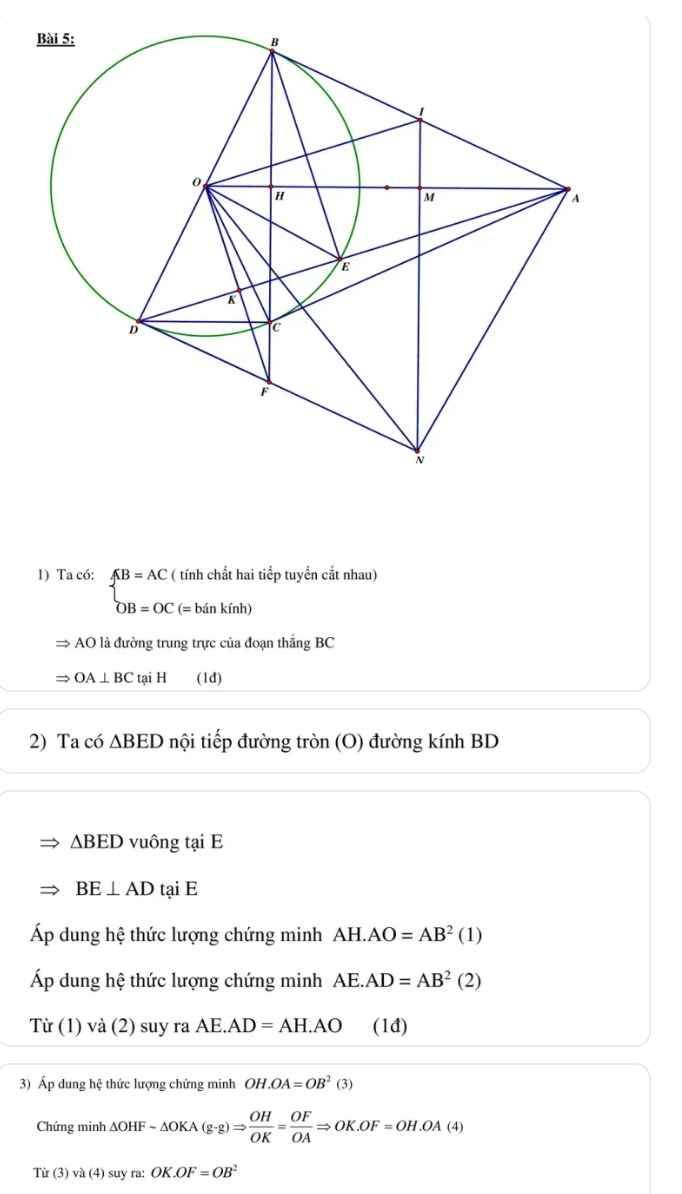
A O B C H D N K I
a/
Xét tg vuông AOB và tg vuông AOC có
\(OB=OC=R;OA\) chung => tg AOB = tg AOC (2 tg vuông có cạnh huyền và cạnh góc vuông tương ứng = nhau)
\(\Rightarrow AB=AC\) => tg ABC cân tại A và \(\widehat{OAB}=\widehat{OAC}\)
\(\Rightarrow OA\perp BC\) (Trong tg cân đường phân giác của góc ở đỉnh đồng thời là đường cao)
\(\widehat{BCD}=90^o\) (góc nt chắn nửa đường tròn) \(\Rightarrow CD\perp BC\)
=> OA//CD (cùng vg với BC)
b/
Xét tg vuông AOB có
\(OB^2=OH.OA\) (trong tg vuông bình phương 1 cạnh góc vuông bằng tích giữa hình chiếu cạnh góc vuông đó trên cạnh huyền với cạnh huyền)
Ta có
\(\dfrac{OB}{BD}=\dfrac{R}{2R}=\dfrac{1}{2}\Rightarrow OB=\dfrac{BD}{2}\)
\(\Rightarrow\left(\dfrac{BD}{2}\right)^2=OH.OA\Rightarrow4OH.OA=BD^2\)
c/
Xét tg vuông AOC có
\(AC^2=AH.AO\) (trong tg vuông bình phương 1 cạnh góc vuông bằng tích giữa hình chiếu cạnh góc vuông đó trên cạnh huyền với cạnh huyền) (1)
Xét tg ACN và tg ADC có
\(\widehat{CAD}\) chung
\(sđ\widehat{ACN}=\dfrac{1}{2}sđcungCN\) (góc giữa tt và dây cung)
\(sđ\widehat{ADC}=\dfrac{1}{2}sđcungCN\) (góc nt đường tròn)
\(\Rightarrow\widehat{ACN}=\widehat{ADC}\)
=> tg ACN đồng dạng với tg ADC (g.g.g)
\(\Rightarrow\dfrac{AN}{AC}=\dfrac{AC}{AD}\Rightarrow AC^2=AN.AD\) (2)
Từ (1) và (2) \(\Rightarrow AN.AD=AH.AO\)
a: Xét (O) có
AB,AC là các tiếp tuyến
Do đó: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1),(2) suy ra OA là đường trung trực của BC
=>OA\(\perp\)BC tại H và H là trung điểm của BC
Xét (O) có
ΔBCD nội tiếp
BD là đường kính
Do đó: ΔBCD vuông tại C
=>CB\(\perp\)CD
mà OA\(\perp\)BC
nên OA//CD
b: Xét ΔBOA vuông tại B có BH là đường cao
nên \(OH\cdot OA=OB^2\)
=>\(4\cdot OH\cdot OA=4\cdot OB^2=\left(2OB\right)^2=BD^2\)
c: Xét (O) có
ΔBND nội tiếp
BD là đường kính
Do đó: ΔBND vuông tại N
=>BN\(\perp\)AD tại N
Xét ΔBAD vuông tại B có BN là đường cao
nên \(AN\cdot AD=AB^2\left(3\right)\)
Xét ΔABO vuông tại B có BH là đường cao
nên \(AH\cdot AO=AB^2\left(4\right)\)
Từ (3),(4) suy ra \(AN\cdot AD=AH\cdot AO\)
d: Gọi E là giao điểm của DC và BA
Ta có: CK\(\perp\)BD
EB\(\perp\)ED
Do đó: CK//EB
Ta có: ΔBCD vuông tại C
=>BC\(\perp\)DE tại C
=>ΔBCE vuông tại C
Ta có: \(\widehat{CBE}+\widehat{CEB}=90^0\)(ΔCEB vuông tại C)
\(\widehat{ACB}+\widehat{ACE}=\widehat{BCE}=90^0\)
mà \(\widehat{ACB}=\widehat{ABC}\)
nên \(\widehat{ACE}=\widehat{AEC}\)
=>AC=AE
mà AC=AB
nên AE=AB(5)
Xét ΔDAE có CI//AE
nên \(\dfrac{CI}{AE}=\dfrac{DI}{DA}\left(6\right)\)
Xét ΔDBA có KI//BA
nên \(\dfrac{KI}{BA}=\dfrac{DI}{DA}\left(7\right)\)
Từ (5),(6),(7) suy ra CI=IK