Từ điểm M ngoài đường tròn (O;R), vẽ hai tiếp tuyến MA,MB đến đường tròn (O) (A,B là 2 tiếp điểm). Vẽ đường kính AC,MC cắt đường tròn (O) tại D.
a) Chứng minh OM \(\perp\) AB tại H và BC // MO
b) Qua O vẽ đường thắng vuông góc với CD tại I, đường thẳng này cắt AB tại N. Chứng minh: OI . ON = OH . OM và \(\widehat{OAI}\) = \(\widehat{ONA}\)
c) Chứng minh NC là tiếp tuyến của...
Đọc tiếp
Từ điểm M ngoài đường tròn (O;R), vẽ hai tiếp tuyến MA,MB đến đường tròn (O) (A,B là 2 tiếp điểm). Vẽ đường kính AC,MC cắt đường tròn (O) tại D.
a) Chứng minh OM \(\perp\) AB tại H và BC // MO
b) Qua O vẽ đường thắng vuông góc với CD tại I, đường thẳng này cắt AB tại N. Chứng minh: OI . ON = OH . OM và \(\widehat{OAI}\) = \(\widehat{ONA}\)
c) Chứng minh NC là tiếp tuyến của (O)
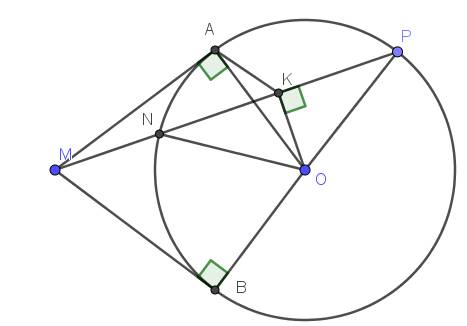
M A B O C D H N I
a/
Xét tg vuông AMO và tg vuông BMO có
MA=MB (2 tiếp tuyến cùng xp từ 1 điểm ....)
MO chung
=> tg AMO = tg BMO (2 tg vuông có cạnh huyền và cạnh góc vuông tương ứng bằng nhau)
\(\Rightarrow\widehat{AMO}=\widehat{BMO}\)
Xét tg AMB có
MA=MB (cmt) => tg AMB cân tại M
\(\widehat{AMO}=\widehat{BMO}\left(cmt\right)\)
\(\Rightarrow OM\perp AB\) (trong tg cân đường phân giác của góc ở đỉnh đồng thời là đường cao)
b/
Xét tg vuong OIM và tg vuông OHN có
\(\widehat{MON}\) chung
=> tg OIM đồng dạng với tg OHN
\(\Rightarrow\dfrac{OI}{OH}=\dfrac{OM}{ON}\Rightarrow OI.ON=OH.OM\)
tg OIM đồng dạng với tg OHN (cmt) \(\Rightarrow\widehat{ONA}=\widehat{OMI}\)
Ta có A và I cùng nhìn OM dưới 2 góc bằng nhau và \(=90^o\)
=> AOIM là tứ giác nt
\(\Rightarrow\widehat{OAI}=\widehat{OMI}\) (góc nt cùng chắn cung OI)
\(\Rightarrow\widehat{OAI}=\widehat{ONA}=\widehat{OMI}\)
c/
a: Xét (O) có
MA,MB là các tiếp tuyến
Do đó: MA=MB
=>M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1),(2) suy ra MO là đường trung trực của AB
=>MO\(\perp\)AB tại H và H là trung điểm của AB
Xét (O) có
ΔABC nội tiếp
AC là đường kính
Do đó: ΔABC vuông tại B
=>AB\(\perp\)BC
mà MO\(\perp\)AB
nên MO//BC
b: Xét ΔOHN vuông tại H và ΔOIM vuông tại I có
\(\widehat{HON}\) chung
Do đó: ΔOHN~ΔOIM
=>\(\dfrac{OH}{OI}=\dfrac{ON}{OM}\)
=>\(OH\cdot OM=OI\cdot ON\)
Xét ΔOAM vuông tại A có AH là đường cao
nên \(OH\cdot OM=OA^2\)
=>\(OI\cdot ON=OA^2\)
=>\(\dfrac{OI}{OA}=\dfrac{OA}{ON}\)
Xét ΔOIA và ΔOAN có
\(\dfrac{OI}{OA}=\dfrac{OA}{ON}\)
\(\widehat{IOA}\) chung
Do đó: ΔOIA~ΔOAN
=>\(\widehat{OAI}=\widehat{ONA}\)
c: Ta có: \(OA^2=OI\cdot ON\)
mà OC=OA(=R)
nên \(OC^2=OI\cdot ON\)
=>\(\dfrac{OC}{OI}=\dfrac{ON}{OC}\)
Xét ΔOCN và ΔOIC có
\(\dfrac{OC}{OI}=\dfrac{ON}{OC}\)
\(\widehat{CON}\) chung
Do đó: ΔOCN~ΔOIC
=>\(\widehat{OCN}=\widehat{OIC}\)
=>\(\widehat{OCN}=90^0\)
=>NC là tiếp tuyến của (O)