PT đa thức thành nhân tử:
(x-1)(x-3)(x+2)(x+4)+21
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: \(A=2\left(x+y\right)^4-3\left(x+y\right)^2-5\)
\(=2\left(x+y\right)^4-5\left(x+y\right)^2+2\left(x+y\right)^2-5\)
\(=\left(x+y\right)^2\left[2\left(x+y\right)^2-5\right]+\left[2\left(x+y\right)^2-5\right]\)
\(=\left[2\left(x+y\right)^2-5\right]\left[\left(x+y\right)^2+1\right]\)

\(1,\\ a,=4\left(x-2\right)^2+y\left(x-2\right)=\left(4x-8+y\right)\left(x-2\right)\\ b,=3a^2\left(x-y\right)+ab\left(x-y\right)=a\left(3a+b\right)\left(x-y\right)\\ 2,\\ a,=\left(x-y\right)\left[x\left(x-y\right)^2-y-y^2\right]\\ =\left(x-y\right)\left(x^3-2x^2y+xy^2-y-y^2\right)\\ b,=2ax^2\left(x+3\right)+6a\left(x+3\right)\\ =2a\left(x^2+3\right)\left(x+3\right)\\ 3,\\ a,=xy\left(x-y\right)-3\left(x-y\right)=\left(xy-3\right)\left(x-y\right)\\ b,Sửa:3ax^2+3bx^2+ax+bx+5a+5b\\ =3x^2\left(a+b\right)+x\left(a+b\right)+5\left(a+b\right)\\ =\left(3x^2+x+5\right)\left(a+b\right)\\ 4,\\ A=\left(b+3\right)\left(a-b\right)\\ A=\left(1997+3\right)\left(2003-1997\right)=2000\cdot6=12000\\ 5,\\ a,\Leftrightarrow\left(x-2017\right)\left(8x-2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=2017\\x=\dfrac{1}{4}\end{matrix}\right.\\ b,\Leftrightarrow\left(x-1\right)\left(x^2-16\right)=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=4\\x=-4\end{matrix}\right.\)

xin loi bn nha
mk moi chi hok lop 6
mk nghi bn nen tu lam thi hon,ko nen dua vao olm.vn qua
chuc bn hok tot nha

x3 - 5x2 + x - 5 = (x3 - 5x2) + (x - 5) = x2(x - 5) + (x - 5) = (x - 5)(x2 + 1)
cho mk hỏi rút gọn bt nay nhé A= 1phần x+1 trừ x-1phân x cộng x+2 phần x^2 +x

x^8+x+1= (x^8 - x^5) + (x^5 - x^2) + (x^2+x+1)
= x^5.(x^3-1) + x^2.(x^3-1) + (x^2+x+1)
= x^5.(x-1).(x^2+x+1) + x^2.(x-1).(x^2+x+1) + (x^2+x+1)
=(x^2+x+1).[x^5.(x-1)+x^2.(x-1)+1]

d) mk chỉnh lại đề
\(8xy^2-5xyz-24y+15z\)
\(=xy\left(8y-5z\right)-3\left(8y-5z\right)\)
\(=\left(8y-5z\right)\left(xy-3\right)\)
e) \(x^4-x^3-x+1=\left(x-1\right)^2\left(x^2+x+1\right)\)
f) \(x^4+x^2y^2+y^4=\left(x^2-xy+y^2\right)\left(x^2+xy-y^2\right)\)
g) \(x^3+3x-4=\left(x-1\right)\left(x^2+x+4\right)\)
h) \(x^3-3x^2+2=\left(x-1\right)\left(x^2-2x-2\right)\)
i) \(2x^3+x^2-4x-12=\left(x-2\right)\left(2x^2+5x+6\right)\)
k) \(25x^2\left(x-5\right)-x+y=\left(1-5x\right)\left(1+5x\right)\left(y-x\right)\)

\(1,\\ 1,=15\left(x+y\right)\\ 2,=4\left(2x-3y\right)\\ 3,=x\left(y-1\right)\\ 4,=2x\left(2x-3\right)\\ 2,\\ 1,=\left(x+y\right)\left(2-5a\right)\\ 2,=\left(x-5\right)\left(a^2-3\right)\\ 3,=\left(a-b\right)\left(4x+6xy\right)=2x\left(2+3y\right)\left(a-b\right)\\ 4,=\left(x-1\right)\left(3x+5\right)\\ 3,\\ A=13\left(87+12+1\right)=13\cdot100=1300\\ B=\left(x-3\right)\left(2x+y\right)=\left(13-3\right)\left(26+4\right)=10\cdot30=300\\ 4,\\ 1,\Rightarrow\left(x-5\right)\left(x-2\right)=0\Rightarrow\left[{}\begin{matrix}x=2\\x=5\end{matrix}\right.\\ 2,\Rightarrow\left(x-7\right)\left(x+2\right)=0\Rightarrow\left[{}\begin{matrix}x=7\\x=-2\end{matrix}\right.\\ 3,\Rightarrow\left(3x-1\right)\left(x-4\right)=0\Rightarrow\left[{}\begin{matrix}x=\dfrac{1}{3}\\x=4\end{matrix}\right.\\ 4,\Rightarrow\left(2x+3\right)\left(2x-1\right)=0\\ \Rightarrow\left[{}\begin{matrix}x=-\dfrac{3}{2}\\x=\dfrac{1}{2}\end{matrix}\right.\)

21(x-y)2-7(y-x)3
=21(x2-y2)-7(y2-x2)
=21x2-21y2-7y2+7x2
=28x2-28y2
=28(x2-y2)

1)
a) => 16x2 - 8x + 1 - 8(2x2 + 3x - 4x - 6) = 15
=> 16x2 - 8x + 1 - 8(2x2 - x - 6) = 15
=> 16x2 - 8x + 1 - 16x2 + 8x + 48 = 15
=> 49 = 15 (?) (vô lí)
=> Không tìm được x thoả mãn
b) (5x - 2)(x - 2) - 4(x - 3) = x2 + 3
=> 5x2 - 10x - 2x + 4 - 4x + 12 = x2 + 3
=> 5x2 - 16x + 16 = x2 + 3
=> 4x2 - 16x + 16 = 3
=> (2x)2 - 2.2x.4 + 42 = 3
=> (2x - 4)2 = 3
=> \(\left[{}\begin{matrix}2x-4=\sqrt{3}\\2x-4=-\sqrt{3}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=\dfrac{4+\sqrt{3}}{2}\\x=\dfrac{4-\sqrt{3}}{2}\end{matrix}\right.\)
Mong bạn xem lại đề bài!
2)
a) 5x2 - 10xy + 5y2 - 20z2
= 5(x2 - 2xy + y2 - 4z2)
= 5[(x - y)2 - (2z)2]
= 5(x - y - 2z)(x - y + 2z)
b) a3 - ay - a2x + xy
= a(a2 - y) - x(a2 - y)
= (a - x)(a2 - y)
c) 3x2 - 6xy + 3y2 - 12z2
= 3(x2 - 2xy + y2 - 4z2)
= 3[(x - y)2 - (2z)2]
= 3(x - y - 2z)(x - y + 2z)
d) x2 - 2xy + tx - 2ty
= x(x - 2y) + t(x - 2y)
= (x + t)(x - 2y)
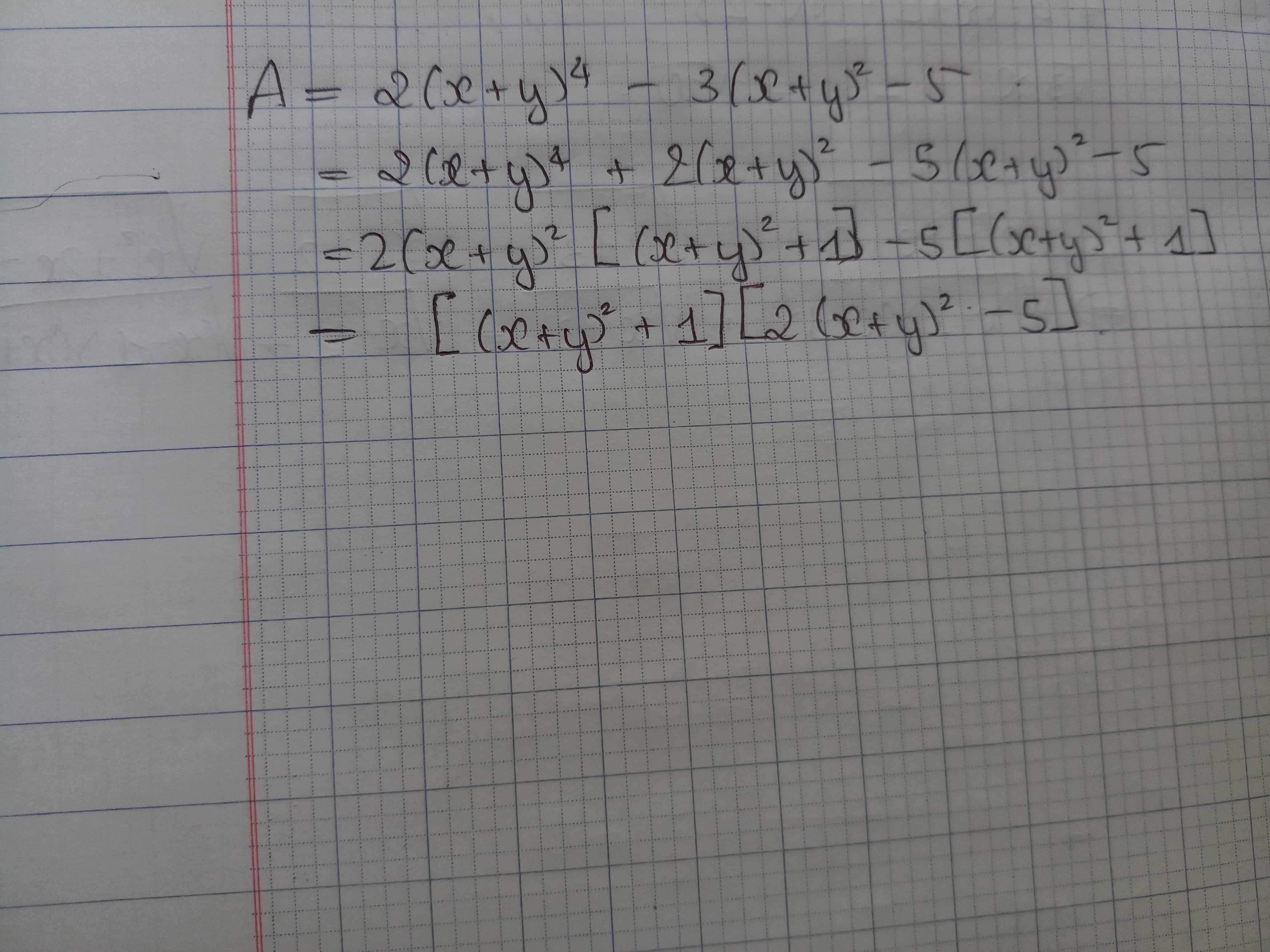
(x-1)(x-3)(x+2)(x+4)+21
\(=\left(x-1\right)\left(x+2\right)\left(x-3\right)\left(x+4\right)+21\)
\(=\left(x^2+x-2\right)\left(x^2+x-12\right)+21\)
\(=\left(x^2+x\right)^2-14\left(x^2+x\right)+24+21\)
\(=\left(x^2+x\right)^2-14\left(x^2+x\right)+45\)
\(=\left(x^2+x-5\right)\left(x^2+x-9\right)\)
Chúng ta có biểu thức:
(x−1)(x−3)(x+2)(x+4)+21(x-1)(x-3)(x+2)(x+4) + 21Bước 1: Tính (x−1)(x−3)=x2−4x+3(x-1)(x-3) = x^2 - 4x + 3 và (x+2)(x+4)=x2+6x+8(x+2)(x+4) = x^2 + 6x + 8.
Bước 2: Nhân hai kết quả lại:
(x2−4x+3)(x2+6x+8)=x4+2x3−13x2−14x+24(x^2 - 4x + 3)(x^2 + 6x + 8) = x^4 + 2x^3 - 13x^2 - 14x + 24Bước 3: Thêm 21 vào:
x4+2x3−13x2−14x+24+21=x4+2x3−13x2−14x+45x^4 + 2x^3 - 13x^2 - 14x + 24 + 21 = x^4 + 2x^3 - 13x^2 - 14x + 45Vậy, biểu thức đã phân tích là:
(x−1)(x−3)(x+2)(x+4)+21=x4+2x3−13x2−14x+45