Giúp em hiểu với ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
2
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 7 2021
1.
Xét pt đầu:
\(x^2-xy+x-y=0\)
\(\Leftrightarrow x\left(x-y\right)+x-y=0\)
\(\Leftrightarrow\left(x+1\right)\left(x-y\right)=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=y\end{matrix}\right.\)
TH1: \(x=-1\) thay xuống pt dươi:
\(\sqrt{y^2+15}=-3-2+\sqrt{9}\Leftrightarrow\sqrt{y^2+15}=-2< 0\) (vô nghiệm)
TH2: thay \(y=x\) xuống pt dưới:
\(\sqrt{x^2+15}=3x-2+\sqrt{x^2+8}\) (1)
\(\Rightarrow3x-2=\sqrt{x^2+15}-\sqrt{x^2+8}=\dfrac{7}{\sqrt{x^2+15}+\sqrt{x^2+8}}>0\)
\(\Rightarrow x>\dfrac{2}{3}\)
Do đó (1) tương đương:
\(3x-2+\sqrt{x^2+8}-\sqrt{x^2+15}=0\)
\(\Leftrightarrow3x-3+\sqrt{x^2+8}-3+4-\sqrt{x^2+15}=0\)
\(\Leftrightarrow3\left(x-1\right)+\dfrac{\left(x-1\right)\left(x+1\right)}{\sqrt{x^2+8}+3}-\dfrac{\left(x-1\right)\left(x+1\right)}{\sqrt{x^2+15}+4}=0\)
\(\Leftrightarrow\left(x-1\right)\left[3+\left(x+1\right)\left(\dfrac{1}{\sqrt{x^2+8}+3}-\dfrac{1}{\sqrt{x^2+15}+4}\right)\right]=0\)
\(\Leftrightarrow x-1=0\) (do \(x+1>0\) nên ngoặc phía sau luôn dương)
\(\Leftrightarrow x=y=1\)
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 7 2021
2.
Pt đầu tương đương:
\(y^2-x+x^2-2xy+x=0\)
\(\Leftrightarrow\left(x-y\right)^2=0\Leftrightarrow y=x\)
Thay xuống pt dưới:
\(2x^2+x-x^2+x-3=0\)
\(\Leftrightarrow x^2+2x-3=0\)
\(\Rightarrow\left[{}\begin{matrix}x=1\Rightarrow y=1\\x=-3\Rightarrow y=-3\end{matrix}\right.\)
10 tháng 10 2021
\(B=\sqrt{\dfrac{1}{3}}+\dfrac{\sqrt{3}-1}{\sqrt{3}+1}+\dfrac{2}{\sqrt{3}}-\dfrac{3-\sqrt{3}}{\sqrt{3}-1}\)
\(\Rightarrow B=\dfrac{\sqrt{1}}{\sqrt{3}}+\dfrac{\left(\sqrt{3}-1\right)^2}{\left(\sqrt{3}+1\right)\left(\sqrt{3}-1\right)}+\dfrac{2}{\sqrt{3}}-\dfrac{\sqrt{3}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}\)
\(\Rightarrow B=\left(\dfrac{1}{\sqrt{3}}+\dfrac{2}{\sqrt{3}}\right)+\dfrac{3-2\sqrt{3}+1}{\left(\sqrt{3}+1\right)\left(\sqrt{3}-1\right)}-\sqrt{3}\)
\(\Rightarrow B=\dfrac{3}{\sqrt{3}}+\dfrac{4-2\sqrt{3}}{\left(\sqrt{3}+1\right)\left(\sqrt{3}-1\right)}-\sqrt{3}\)
\(\Rightarrow B=\sqrt{3}+\dfrac{4-2\sqrt{3}}{\sqrt{3^2}-1^2}-\sqrt{3}\)
\(\Rightarrow B=\dfrac{4-2\sqrt{3}}{2}\)
\(\Rightarrow B=2-\sqrt{3}\)
HN
10 tháng 10 2021
⇔ \(B=\dfrac{1}{\sqrt{3}}+\dfrac{\left(\sqrt{3}-1\right)\left(\sqrt{3}-1\right)}{\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)}+\dfrac{2}{\sqrt{3}}-\dfrac{\sqrt{3}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}\)
⇔ \(B=\dfrac{\text{3}}{\sqrt{3}}+\dfrac{3-2\sqrt{3}+1}{3-1}-\sqrt{3}\)
⇔ \(B=\sqrt{3}+\dfrac{\text{4}-2\sqrt{3}}{\text{2}}-\sqrt{3}\)
⇔ \(B=\dfrac{2\left(2-\sqrt{3}\right)}{2}=2-\sqrt{3}\)
NT
0
AF
1
LY
1
22 tháng 11 2021
Câu 14 : Kẽm đẩy sắt ra khỏi dung dịch FeCl2 thì :
A Sắt có thể đẩy kẽm ra khỏi dung dịch ZnCl2
B Sắt hoạt động hóa học mạnh hơn kẽm
C Sắt đứng sau kẽm trong dãy hoạt động hóa học
D Kẽm hoạt động hóa học mạnh hơn sắt
Pt : \(Zn+FeCl_2\rightarrow ZnCl_2+Fe\)
Chúc bạn học tốt
ND
29 tháng 10 2019
https://olm.vn/tin-tuc /Bat-dang-thuc-Cauchy-(-Co-si)
#Trang
ND
29 tháng 10 2019
Bất đẳng thức Cauchy ( Cô-si) - Học toán với OnlineMath
#Trang
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 11 2021
11c.
Từ đề bài ta có:
\(\left\{{}\begin{matrix}\dfrac{16a-b^2}{4a}=\dfrac{9}{2}\\16a+4b+4=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2b^2=-4a\\b=-4a-1\end{matrix}\right.\)
\(\Rightarrow2b^2-b=1\Leftrightarrow2b^2-b-1=0\Rightarrow\left[{}\begin{matrix}b=1\Rightarrow a=-\dfrac{1}{2}\\b=-\dfrac{1}{2}\Rightarrow a=-\dfrac{1}{8}\end{matrix}\right.\)
Có 2 parabol thỏa mãn: \(\left[{}\begin{matrix}y=-\dfrac{1}{2}x^2+x+4\\y=-\dfrac{1}{8}x^2-\dfrac{1}{2}x+4\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 11 2021
4f.
Từ đề bài ta có:
\(\left\{{}\begin{matrix}1+b+c=0\\\dfrac{4c-b^2}{4}=-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}c=-b-1\\c=\dfrac{b^2}{4}-1\end{matrix}\right.\)
\(\Rightarrow\dfrac{b^2}{4}+b=0\)
\(\Rightarrow\left[{}\begin{matrix}b=0\Rightarrow c=-1\\b=-4\Rightarrow c=3\end{matrix}\right.\)
Có 2 parabol thỏa mãn: \(\left[{}\begin{matrix}y=x^2-1\\y=x^2-4x+3\end{matrix}\right.\)
TQ
0
NT
1
DT
Đỗ Thanh Hải
CTVVIP
1 tháng 8 2021
52 vegetarians
53 entrance
54 modernized
55 income
56 opposite
57 Comsumers
58 disatisfaction
59 Conservation
60 practices (nghe k hợp lắm)
nếu có thêm use thì là practical
61 inspiration
62 unfriendly
63 disagree
64 comparision
65 bored
66 unsuccessful
67 readiness
68 poverty
69 carelessly
70 mountainous
71 unemployment
72 examination
73 multinational
74 positivity
75 respectful
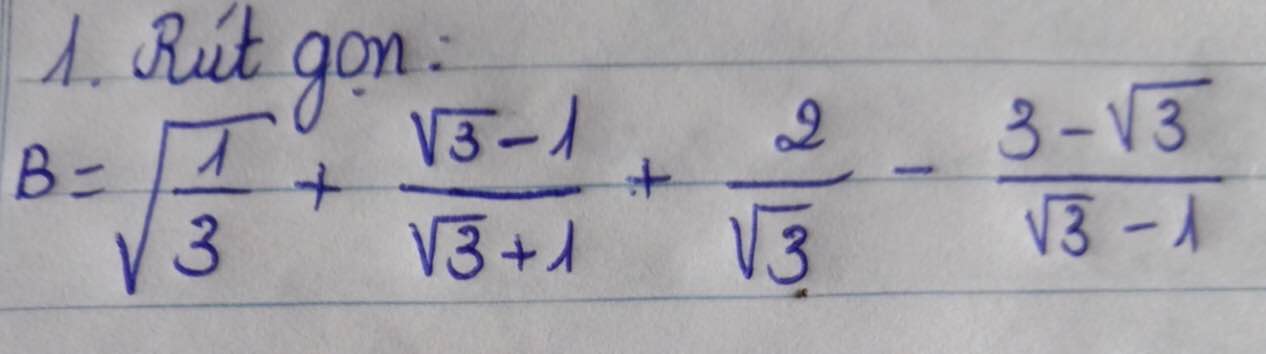
phần a bạn chỉ cần tính đạo hàm, xong cho y'=0 tính nghiệm, ra nghiệm vẽ bảng biến thiên xét dấu( cách tính đạo hàm :đạo hàm của tử nhân mẫu trừ tử nhân mẫu đạo hàm; ra hàm bậc 3 bạn sẽ tính nghiệm xét dấu theo phương pháp trước trái sau cùng hoặc thay giá trị bất kì
phần b khi vẽ được bảng biến thiên sẽ xét được điểm cực tiểu
phần c bạn chỉ cần thực hiện phép chia sẽ ra tiệm cận xiên( lấy tử chia mẫu)
phần d mình chưa biết @@
nếu bạn chưa hiểu phần trên muốn biết rõ hơn hãy liên hệ phuongthuytctdbg8@gmail.com, mình sẽ hướng dẫn rõ hơn