(\(\dfrac{1}{4}\)x-\(\dfrac{2}{5}\))(\(\dfrac{2}{7}x+\dfrac{3}{4}\))=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
29 tháng 10 2021
3: \(\left|x-\dfrac{3}{4}\right|-\dfrac{1}{2}=0\)
\(\Leftrightarrow\left|x-\dfrac{3}{4}\right|=\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{3}{4}=\dfrac{1}{2}\\x-\dfrac{3}{4}=-\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{4}\\x=\dfrac{1}{4}\end{matrix}\right.\)
18 tháng 9 2021
1) \(\dfrac{11}{12}-\left(\dfrac{2}{5}+x\right)=\dfrac{2}{3}\)
\(\Leftrightarrow\dfrac{11}{12}-\dfrac{2}{5}-x=\dfrac{2}{3}\)
\(\Leftrightarrow x=\dfrac{11}{12}-\dfrac{2}{5}-\dfrac{2}{3}\)
\(\Leftrightarrow x=-\dfrac{3}{20}\)
2) \(2x\left(x-\dfrac{1}{7}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=0\\x-\dfrac{1}{7}=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{1}{7}\end{matrix}\right.\)
3) \(\dfrac{3}{4}+\dfrac{1}{4}:x=\dfrac{2}{5}\)
\(\Leftrightarrow\dfrac{1}{4x}=\dfrac{2}{5}-\dfrac{3}{4}\)
\(\Leftrightarrow\dfrac{1}{4x}=-\dfrac{7}{20}\)
\(\Leftrightarrow4x=-\dfrac{20}{7}\)
\(\Leftrightarrow x=-\dfrac{5}{7}\)
29 tháng 1 2022
a: =>1/2x=7/2-2/3=21/6-4/6=17/6
=>x=17/3
b: =>2/3:x=-7-1/3=-22/3
=>x=2/3:(-22/3)=-1/11
c: =>1/3x+2/5x-2/5=0
=>11/15x=2/5
hay x=6/11
d: =>2x-3=0 hoặc 6-2x=0
=>x=3/2 hoặc x=3
NH
11 tháng 3 2023
bạn tách một câu vài câu hỏi chứ đừng gộp như thế này ko ai trả lời đâu
11 tháng 3 2023
a: =>\(4x-5=2x-2+x=3x-2\)
=>x=3
b: \(\Leftrightarrow7x-35=3x+6\)
=>4x=41
=>x=41/4
c: =>(2x+5)(x+5)-2x^2=0
=>2x^2+10x+5x+25-2x^2=0
=>15x=-25
=>x=-5/3
e: \(\Leftrightarrow\dfrac{11}{x}=\dfrac{9x-36+2x+2}{\left(x+1\right)\left(x-4\right)}\)
=>11(x^2-3x-4)=x(11x-34)
=>11x^2-33x-44=11x^2-34x
=>x=44
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
27 tháng 8 2023
a, - \(\dfrac{2}{5}\) + \(\dfrac{4}{5}\).\(x\) = \(\dfrac{3}{5}\)
\(\dfrac{4}{5}\).\(x\) = \(\dfrac{3}{5}\)+ \(\dfrac{2}{5}\)
\(\dfrac{4}{5}\).\(x\) = 1
\(x\) = \(\dfrac{5}{4}\)
b, - \(\dfrac{3}{7}\) - \(\dfrac{4}{7}\): \(x\) = \(\dfrac{2}{5}\)
\(\dfrac{4}{7}\): \(x\) = - \(\dfrac{3}{7}\) - \(\dfrac{2}{5}\)
\(\dfrac{4}{7}\): \(x\) = - \(\dfrac{29}{35}\)
\(x\) = \(\dfrac{4}{7}\): (- \(\dfrac{29}{35}\) )
\(x\) = - \(\dfrac{20}{29}\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
27 tháng 8 2023
c, \(\dfrac{4}{7}\).\(x\) + \(\dfrac{2}{3}\) = - \(\dfrac{1}{5}\)
\(\dfrac{4}{7}\).\(x\) = -\(\dfrac{1}{5}\) - \(\dfrac{2}{3}\)
\(\dfrac{4}{7}\).\(x\) = - \(\dfrac{13}{15}\)
\(x\) = - \(\dfrac{13}{15}\): \(\dfrac{4}{7}\)
\(x\) = - \(\dfrac{91}{60}\)
12 tháng 1 2018
2, \(\Rightarrow\left\{{}\begin{matrix}\\\dfrac{5}{4}x-\dfrac{7}{2}=0\\\dfrac{5}{8}x+\dfrac{3}{5}=0\\\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{14}{5}\\\\x=\dfrac{-24}{25}\\\end{matrix}\right.\)
15 tháng 5 2022
a: (x+1/2)(2/3-2x)=0
=>x+1/2=0 hoặc 2/3-2x=0
=>x=-1/2 hoặc x=1/3
b: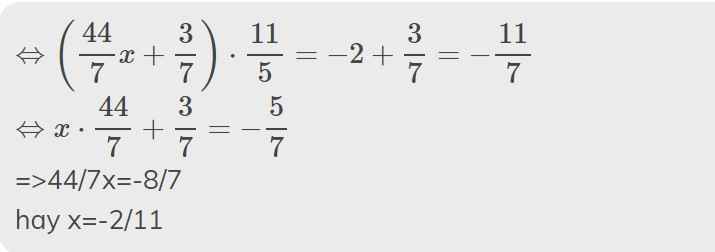 
c: \(\Leftrightarrow x\cdot\left(\dfrac{13}{4}-\dfrac{7}{6}\right)=\dfrac{5}{12}+\dfrac{5}{3}=\dfrac{5}{12}+\dfrac{20}{12}=\dfrac{25}{12}\)
\(\Leftrightarrow x=\dfrac{25}{12}:\dfrac{39-14}{12}=\dfrac{25}{25}=1\)
H
16 tháng 10 2023
`3/5 : x =1/3 +1/2`
` 3/5 : x= 2/6 +3/6`
` 3/5 : x= 5/6`
` x= 3/5 : 5/6`
` x= 3/5 xx 6/5`
` x= 18/25`
__
`x: 7/15 =2`
` x= 2xx 7/15`
` x= 14/15`
__
`x-3/2=11/4-5/4`
`x-3/2= 6/4`
`x= 3/2 +3/2`
`x= 6/2`
`x=3`
__
`x+5/4 = 3/2+7/12`
`x+5/4 = 18/12+7/12`
`x+5/4 = 25/12`
`x= 25/12-5/4`
`x= 25/12- 15/12`
`x= 10/12`
`x= 5/6`
28 tháng 2 2022
a: =>x-3/4=1/6-1/2=1/6-3/6=-2/6=-1/3
=>x=-1/3+3/4=-4/12+9/12=5/12
b: =>x(1/2-5/6)=7/2
=>-1/3x=7/2
hay x=-21/2
c: (4-x)(3x+5)=0
=>4-x=0 hoặc 3x+5=0
=>x=4 hoặc x=-5/3
d: x/16=50/32
=>x/16=25/16
hay x=25
e: =>2x-3=-1/4-3/2=-1/4-6/4=-7/4
=>2x=-7/4+3=5/4
hay x=5/8
27 tháng 8 2023
a, 2/5 + 3/4 : x = -1/2
3/4 : x = -1/2 - 2/5
3/4 : x = -9/10
x = 3/4 : -9/10
x = -5/6
27 tháng 8 2023
b, 5/7 - 2/3 . x = 4/5
2/3 . x = 4/5 + 5/7
2/3 . x = 53/35
x = 53/35 : 2/3
x = 159/70
\(\left(\dfrac{1}{4}x-\dfrac{2}{5}\right)\left(\dfrac{2}{7}x+\dfrac{3}{4}\right)=0\\ \Rightarrow\left[{}\begin{matrix}\dfrac{1}{4}x-\dfrac{2}{5}=0\\\dfrac{2}{7}x+\dfrac{3}{4}=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}\dfrac{1}{4}x=\dfrac{2}{5}\\\dfrac{2}{7}x=-\dfrac{3}{4}\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=\dfrac{2}{5}:\dfrac{1}{4}\\x=-\dfrac{3}{4}:\dfrac{2}{7}\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=\dfrac{8}{5}\\x=-\dfrac{21}{8}\end{matrix}\right.\)
Vậy...