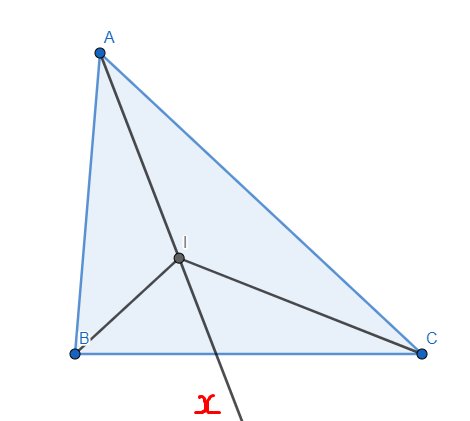
cho ABC. Hai đường phân giác Của góc B và góc C cắt nhau ở I. CTR BIC=90+ A/2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 7 2023
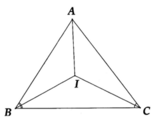
Kẻ tia phân giác Ax của tam giác ABC. Theo tính chất góc ngoài của tam giác, dễ có \(\widehat{BIx}=\widehat{IBA}+\widehat{IAB}\) và \(\widehat{CIx}=\widehat{ICA}+\widehat{IAC}\). Cộng theo vế 2 đẳng thức trên, thu được \(\widehat{BIC}=\dfrac{\widehat{ABC}}{2}+\dfrac{\widehat{ACB}}{2}+\widehat{ABC}\) \(=\dfrac{180^o+\widehat{ABC}}{2}\) \(=90^o+\dfrac{\widehat{BAC}}{2}\)
Tới đây mình cũng đã chứng minh xong câu b luôn rồi. Bạn chỉ cần thay số đo góc vào thì tính được câu a.
3 tháng 7 2023
a) (BI và CI lần lượt là các đường phân giác của góc B và C)
Theo đề ta có:
\(\widehat{IBC}+\widehat{ICB}+\widehat{BIC}=180^o\)
\(\Leftrightarrow\widehat{IBC}+\widehat{ICB}=180^o-\widehat{BIC}=180^o-140^o=40^o\)
Mà \(\widehat{ABI}=\widehat{CBI}\) và \(\widehat{ACI}=\widehat{BCI}\) (vì BI và CI lần lượt là các đường phân giác của góc B và C)
Suy ra \(\widehat{ABC}+\widehat{ACB}=2\widehat{IBC}+2\widehat{ICB}=2\left(\widehat{IBC}+\widehat{ICB}\right)=2\cdot40^o=80^o\)
Từ đó
\(\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=180^o\)
\(\Leftrightarrow\widehat{BAC}=180^o-\left(\widehat{ABC}+\widehat{ACB}\right)=180^o-80^o=100^o\)
HN
1
15 tháng 8 2021
Xét ΔABC có
\(\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=180^0\)
\(\Leftrightarrow2\cdot\left(\widehat{IBC}+\widehat{ICB}\right)=180^0-\widehat{A}\)
\(\Leftrightarrow\widehat{IBC}+\widehat{ICB}=\dfrac{180^0-\widehat{A}}{2}\)
Xét ΔIBC có
\(\widehat{BIC}+\widehat{IBC}+\widehat{ICB}=180^0\)
\(\Leftrightarrow\widehat{BIC}=180^0-90^0+\dfrac{\widehat{A}}{2}\)
\(\Leftrightarrow\widehat{BIC}=90^0+\dfrac{\widehat{A}}{2}\)
DY
1
18 tháng 8 2015
A B C I 1 1 1
Trong tam giác BIC có góc B1 + góc C1 + góc I1 = 180 độ
\(\Rightarrow\) góc I1 = 180 độ - (góc B1 + góc C1)
= 180 độ - (góc ABC/2 + góc ACB/2)
= 180 độ - (góc ABC + góc ACB)/2
= 180 độ - (180 độ - góc A)/2
= 180 độ - (90 độ/2)
= 180 độ - 45 độ
= 135 độ
Vậy góc BIC = 135 độ
CTR BIC + 90 A/2 là sao?
Mình k hiểu
A B C I
xét \(\Delta ABC\)có : \(\widehat{A}+\widehat{ABC}+\widehat{ACB}=180^o\)\(\Rightarrow\widehat{ABC}+\widehat{ACB}=180^o-\widehat{A}\)
xét \(\Delta BIC\)có : \(\widehat{IBC}+\widehat{ICB}+\widehat{BIC}=180^o\)\(\Rightarrow180^o-\left(\widehat{ICB}+\widehat{IBC}\right)=\widehat{BIC}\)
Mà \(\widehat{IBC}=\frac{\widehat{ABC}}{2};\widehat{ICB}=\frac{\widehat{ABC}}{2}\)
\(\Rightarrow\)\(180^o-\left(\frac{\widehat{ABC}}{2}+\frac{\widehat{ACB}}{2}\right)=\widehat{BIC}\)
\(\Rightarrow180^o-\left(\frac{\widehat{ABC}+\widehat{ACB}}{2}\right)=\widehat{BIC}\)
\(\Rightarrow180^o-\left(\frac{180^o-\widehat{A}}{2}\right)=\widehat{BIC}\)
\(\Rightarrow180^o-\frac{180^o}{2}+\frac{\widehat{A}}{2}=\widehat{BIC}\)
\(\Rightarrow\widehat{BIC}=90^o+\frac{\widehat{A}}{2}\)