
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


2:
a: BC=căn 15^2+20^2=25cm
AH=15*20/25=12cm
góc ADH=góc AEH=góc DAE=90 độ
=>ADHE là hình chữ nhật
=>DE=AH=12cm
b: ΔAHB vuông tại H có HD vuông góc AB
nên AD*AB=AH^2
ΔAHC vuông tại H có HE vuông góc AC
nên AE*AC=AH^2
=>AD*AB=AE*AC
c: góc IAC+góc AED
=góc ICA+góc AHD
=góc ACB+góc ABC=90 độ
=>AI vuông góc ED
4:
a: góc BDH=góc BEH=góc DBE=90 độ
=>BDHE là hình chữ nhật
b: BDHE là hình chữ nhật
=>góc BED=góc BHD=góc A
Xét ΔBED và ΔBAC có
góc BED=góc A
góc EBD chung
=>ΔBED đồng dạng với ΔBAC
=>BE/BA=BD/BC
=>BE*BC=BA*BD
c: góc MBC+góc BED
=góc C+góc BHD
=góc C+góc A=90 độ
=>BM vuông góc ED

a: (x-4)(x+5)>0
=>x-4>0 hoặc x+5<0
=>x>4 hoặc x<-5
b: (2x+1)(x-3)<0
=>2x+1>0 và x-3<0
=>-1/2<x<3
c: (x-7)(3-x)<0
=>(x-7)(x-3)>0
=>x>7 hoặc x<3
d: x^2+6x-16<0
=>(x+8)(x-2)<0
=>-8<x<2
e: 3x^2+7x+4<0
=>3x^2+3x+4x+4<0
=>(x+1)(3x+4)<0
=>3x+4>0 và x+1<0
=>-4/3<x<-1
f: 5x^2-9x+4>0
=>(x-1)(5x-4)>0
=>x>1 hoặc x<4/5
g: x^2+6x-16<0
=>(x+8)(x-2)<0
=>-8<x<2
h: x^2+4x-21>0
=>(x+7)(x-3)>0
=>x>3 hoặc x<-7
i: x^2-9x-22<0
=>(x-11)(x+2)<0
=>-2<x<11
l: 16x^2+40x+25<0
=>(2x+5)^2<0(loại)
m: 3x^2-4x-4>=0
=>3x^2-6x+2x-4>=0
=>(x-2)(3x+2)>=0
=>x>=2 hoặc x<=-2/3

https://www.google.com.vn/search?q=%E1%BA%A3nh+chibi+d%E1%BB%85+th%C6%B0%C6%A1ng+v%C3%A0+%C4%91%E1%BA%B9p&tbm=isch&tbo=u&source=univ&sa=X&ved=0ahUKEwjd6d2Sga_bAhXEW5QKHWrjDZ0QsAQIIw&biw=1366&bih=663
* Link đó !


Mình xin phép bổ sung một chút vào trong hình vẽ nha bạn. Chứ để như vậy thì ko chứng minh a song song với b đâu
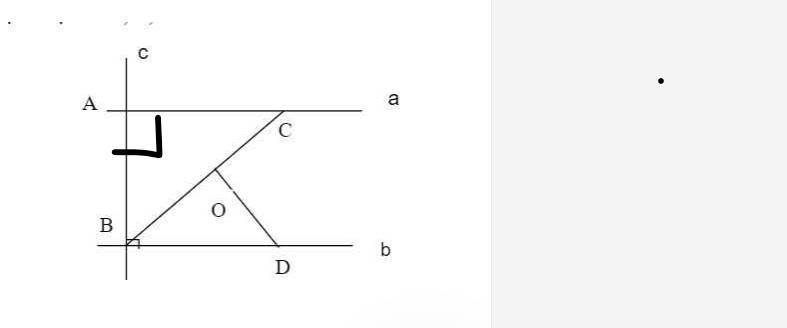
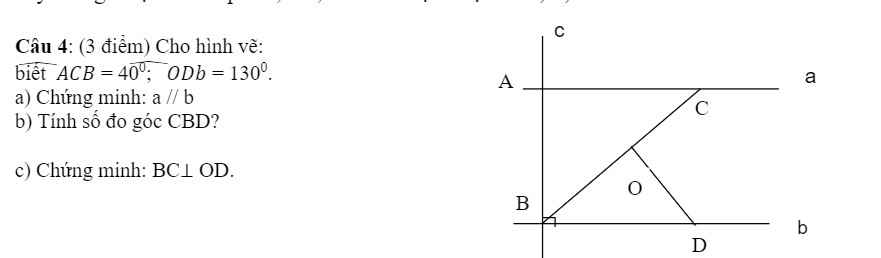
a: a vuông góc AB
b vuông góc AB
=>a//b
b: a//b
=>góc ACB=góc CBD
=>góc CBD=40 độ
c: góc ODB=180-130=50 độ
góc ODB+góc OBD=50+40=90 độ
=>ΔOBD vuông tại O
=>DO vuông góc BC

Ta có:
200920 = 200910.200910 < 200910.1000110 = 2009200910
=> 200920 < 2009200910










 mk vs ạ
mk vs ạ
\(\left(x+2\right)^2\left(y-2\right)+xy^2+26=0\)
\(\Leftrightarrow x^2y-2x^2+xy^2+4xy-8x+4y+18=0\)
\(\Leftrightarrow x^2y-2x^2+4x+xy^2-2xy+4y+6xy-12x+24=6\)
\(\Leftrightarrow x\left(xy-2x+4\right)+y\left(xy-2x+4\right)+6\left(xy-2x+4\right)=6\)
\(\Leftrightarrow\left(x+y+6\right)\left(xy-2x+4\right)=6\)
Ta xét các trường hợp, thu được các nghiệm là:
\(\left(x,y\right)\in\left\{\left(-10,3\right),\left(1,-8\right),\left(-3,3\right),\left(1,-1\right)\right\}\).