công thức tính số số hạng và tổng của một dãy
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a.( số cuối - số đầu): khoảng cách+1
b.(số cuối + số đầu)x số số hạng :2
ai k mik mik k lại
good luck :)

a. Năm số hạng đầu của dãy số
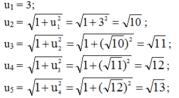
b. Dự đoán công thức số hạng tổng quát của dãy số:
un =√(n+8) (1)
Rõ ràng (1) đúng với n = 1
Giả sử (1) đúng với n = k, nghĩa là uk = √(k+8)
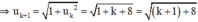
⇒ (1) đúng với n = k + 1
⇒ (1) đúng với mọi n ∈ N*.

* Ta có:
u 2 = 2 u 1 = 2.2 = 4 = 2 2 u 3 = 2 u 2 = 2.4 = 8 = 2 3 u 4 = 2 u 3 = 2.8 = 16 = 2 4 u 5 = 2 u 4 = 2.16 = 32 = 2 5
Từ các số hạng đầu tiên, ta dự đoán số hạng tổng quát u n có dạng: u n = 2 n ∀ n ≥ 1 ∗
* Ta dùng phương pháp chứng minh quy nạp để chứng minh cộng thức (*) đúng.
Với n=1 ; có: u 1 = 2 1 = 2 (đúng). Vậy (*) đúng với n= 1
Giả sử (*) đúng với n= k , có nghĩa ta có: u k = 2 k (2)
Ta cần chứng minh (*) đúng với n = k+1. Có nghĩa là ta phải chứng minh: u k + 1 = 2 k + 1 .
Thật vậy từ hệ thức xác định dãy số và theo (2) ta có:
u k + 1 = 2 u k = 2 . 2 k = 2 k + 1
Vậy (*) đúng với n = k+1. Kết luận (*) đúng với mọi số nguyên dương n.
Chọn đáp án B.

1; Số số hạng = (số cuối - số đầu) : khoảng cách + 1
2; tổng = (số cuối + số đầu)\(\times\) số số hạng : 2
3; số thứ n = khoảng cách \(\times\)(n-1) + số đầu
4 tìm số đó đứng thứ mấy
vị trí của số cần tìm: (số đó - số đầu): khoảng cách + 1
1.SSH = ( SC - SĐ ) : KC + 1
2.T = ( SĐ + SC ) x SSH :2
3.STn = ( n - 1 ) x KC + SĐ
4. Số đó đứng thứ mấy = ( Số đó - SĐ ) : KC +1

Ta có:
u 2 = u 1 + 2 = 3 + 2 = 5.
u 3 = u 2 + 2 = 5 + 2 = 7.
u 4 = u 3 + 2 = 7 + 2 = 9.
u 5 = u 4 + 2 = 9 + 2 = 11.
Từ các số hạng đầu trên, ta dự đoán số hạng tổng quát u n có dạng:
u n = 2 n + 1 ∀ n ≥ 1 ∗
Ta dùng phương pháp chứng minh quy nạp để chứng minh công thức (*) đúng.
Với n =1 ; u 1 = 2 . 1 + 1 = 3 (đúng). Vậy (*) đúng với n =1
Giả sử (*) đúng với n =k. Có nghĩa ta có: u k = 2 k + 1 (2)
Ta cần chứng minh (*) đúng với n = k+1 - có nghĩa là ta phải chứng minh:
u k + 1 = 2(k+1)+1= 2k + 3
Thật vậy từ hệ thức xác định dãy số và theo (2) ta có:
u k + 1 = u k +2 = 2k +1 +2 = 2k + 3
Vậy (*) đúng khi n = k+1 .
Kết luận (*) đúng với mọi số nguyên dương n.
Đáp án B

SSH = ( so cuoi - so dau ) : khoang cach + 1
Tong = ( so dau + so cuoi ) x so so hang : 2
Hok tot
Công thức tính số số hạng: ( Số cuối - số đầu ) : khoảng cách + 1
Công thức tính tổng: ( Số cuối + số đầu ) x khoảng cách : 2