Mọi người ơi giúp em câu 31 với ạ, em gửi lời cảm ơn trước ạ..
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
PT
2
Những câu hỏi liên quan
MV
16 tháng 7 2017
a,
\(C=\dfrac{1}{11}+\dfrac{1}{12}+\dfrac{1}{13}+...+\dfrac{1}{19}\\ C>0+0+0+...+0=0\left(1\right)\)
\(C=\dfrac{1}{11}+\dfrac{1}{12}+\dfrac{1}{13}+...+\dfrac{1}{19}\)
Ta có:
\(\dfrac{1}{11}< \dfrac{1}{10}\\ \dfrac{1}{12}< \dfrac{1}{10}\\ \dfrac{1}{13}< \dfrac{1}{10}\\ ...\\ \dfrac{1}{19}< \dfrac{1}{10}\)
\(\Rightarrow C< \dfrac{1}{10}+\dfrac{1}{10}+\dfrac{1}{10}+...+\dfrac{1}{10}\left(9\text{ phân số }\dfrac{1}{10}\right)\\ C< 9\cdot\dfrac{1}{10}\\ C< \dfrac{9}{10}< 1\left(2\right)\)
Từ (1) và (2) ta có:
\(0< C< 1\)
Rõ ràng \(0\) và \(1\) là hai số nguyên liên tiếp nên \(C\) không phải là số nguyên
Vậy \(C\) không phải là số nguyên (đpcm)
b,
\(D=2\left[\dfrac{1}{3}+\dfrac{1}{15}+\dfrac{1}{35}+...+\dfrac{1}{n\left(n+2\right)}\right]\\ D=\dfrac{2}{3}+\dfrac{2}{15}+\dfrac{2}{35}+...+\dfrac{2}{n\left(n+2\right)}\\ D>0+0+0+...+0=0\left(1\right)\)
Ta có:
\(D=\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+\dfrac{2}{5\cdot7}+...+\dfrac{2}{n\cdot\left(n+2\right)}\\ D=\dfrac{1}{1}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{n}-\dfrac{1}{n+2}\\ D=\dfrac{1}{1}-\dfrac{1}{n+2}\\ D=1-\dfrac{1}{n+2}< 1\left(\text{Vì }n>0\right)\left(2\right)\)
Từ (1) và (2) ta có:
\(0< D< 1\)
Rõ ràng \(0\) và \(1\) là hai số nguyên liên tiếp nên \(D\) không phải là số nguyên
Vậy \(D\) không phải là số nguyên (đpcm)
c,
\(E=\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{2}{7}+\dfrac{2}{9}+\dfrac{2}{11}\\ E=\dfrac{2}{6}+\dfrac{2}{8}+\dfrac{2}{10}+\dfrac{2}{7}+\dfrac{2}{9}+\dfrac{2}{11}\\ E=\dfrac{2}{6}+\dfrac{2}{7}+\dfrac{2}{8}+\dfrac{2}{9}+\dfrac{2}{10}+\dfrac{2}{11}\)
Ta có:
\(\dfrac{2}{6}>\dfrac{2}{12}\\ \dfrac{2}{7}>\dfrac{2}{12}\\ \dfrac{2}{8}>\dfrac{2}{12}\\ ...\\ \dfrac{2}{11}>\dfrac{2}{12}\)
\(\Rightarrow E>\dfrac{2}{12}+\dfrac{2}{12}+\dfrac{2}{12}+\dfrac{2}{12}+\dfrac{2}{12}+\dfrac{2}{12}\\ E>6\cdot\dfrac{2}{12}\\ E>\dfrac{12}{12}=1\left(1\right)\)
Mặt khác ta có:
\(\dfrac{2}{6}>\dfrac{2}{7}\\ \dfrac{2}{6}>\dfrac{2}{8}\\ \dfrac{2}{6}>\dfrac{2}{9}\\ ...\\ \dfrac{2}{6}>\dfrac{2}{11}\)
\(\Rightarrow E< \dfrac{2}{6}+\dfrac{2}{6}+\dfrac{2}{6}+\dfrac{2}{6}+\dfrac{2}{6}+\dfrac{2}{6}\\ E< 6\cdot\dfrac{2}{6}\\ E< 2\left(2\right)\)
Từ (1) và (2) ta có:
\(1< E< 2\)
Rõ ràng \(1\) và \(2\) là hai số nguyên liên tiếp nên \(E\) không phải là số nguyên
Vậy \(E\) không phải là số nguyên (đpcm)
BN
16 tháng 7 2017
c) \(E=\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{2}{7}+\dfrac{2}{9}+\dfrac{2}{11}\)
\(=\dfrac{2}{6}+\dfrac{2}{8}+\dfrac{2}{10}+\dfrac{2}{7}+\dfrac{2}{9}+\dfrac{2}{11}\)
\(=2\left(\dfrac{1}{6}+\dfrac{1}{7}+\dfrac{1}{8}+\dfrac{1}{9}+\dfrac{1}{10}+\dfrac{1}{11}\right)\)
Ta có: \(\dfrac{1}{6}>\dfrac{1}{7}>\dfrac{1}{8}>\dfrac{1}{9}>\dfrac{1}{10}>\dfrac{1}{11}\)
\(\Rightarrow E>2\left(\dfrac{1}{11}+\dfrac{1}{11}+\dfrac{1}{11}+\dfrac{1}{11}+\dfrac{1}{11}+\dfrac{1}{11}\right)=2\left(\dfrac{1}{11}.6\right)=2\cdot\dfrac{6}{11}=\dfrac{12}{11}>1\) (1)
\(E< 2\left(\dfrac{1}{6}+\dfrac{1}{6}+\dfrac{1}{6}+\dfrac{1}{6}+\dfrac{1}{6}+\dfrac{1}{6}\right)=2\left(\dfrac{1}{6}.6\right)=2.1=2\) (2)
Từ (1) và (2) suy ra 1 < E < 2 suy ra E không phải là số nguyên
DN
26 tháng 12 2017
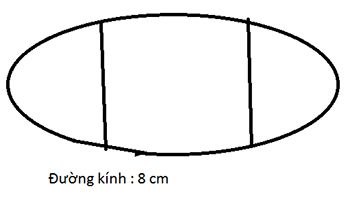
Gọi tứ giác nằm ngang là ABCD.
Hình dựng đứng là ABEMN
Từ điểm M kẻ đường thẳng//AB cắt BE tại G.
Do NM_|_AN tại A
MN//AB; BG//AN
=>BG_|_BE nên tam giác MGE vuông tại G. (1)
=>Tứ giác ABGN là hình chữ nhật=Hình chữ nhật ABCD( vì AB//=CD=14,2 m)
=>AN=AC=5 (m)
Từ (1) =>EG là đường cao của tam giác MGE có cạnh đáy MG.
=>EG=BE-BG=8-5=3 (m)
=>MG=NG-MN=14,2-6,2=8 (m)
Vậy S(MGE)=1/2.EG.MG=1/2.3.8=12 (m2)
=>S(ABCD)+S(ABGN)=2. S(ABCD)
=2.AB.AD=2.5.14,2=142 (m2)
=> Diện tích hình đã cho bằng:
12+142=154 m2
Đ s:
13 tháng 9 2021
Gọi tứ giác nằm ngang là ABCD.
Hình dựng đứng là ABEMN
Từ điểm M kẻ đường thẳng//AB cắt BE tại G.
Do NM_|_AN tại A
MN//AB; BG//AN
=>BG_|_BE nên tam giác MGE vuông tại G. (1)
=>Tứ giác ABGN là hình chữ nhật=Hình chữ nhật ABCD( vì AB//=CD=14,2 m)
=>AN=AC=5 (m)
Từ (1) =>EG là đường cao của tam giác MGE có cạnh đáy MG.
=>EG=BE-BG=8-5=3 (m)
=>MG=NG-MN=14,2-6,2=8 (m)
Vậy S(MGE)=1/2.EG.MG=1/2.3.8=12 (m2)
=>S(ABCD)+S(ABGN)=2. S(ABCD)
=2.AB.AD=2.5.14,2=142 (m2)
=> Diện tích hình đã cho bằng:
12+142=154 m2
LA
14 tháng 12 2017
Giải
Một phần trăm của số học sinh lớp 5B là:
32:100=0,32
Số học sinh thích học toán là:
0,32x75=24 (học sinh)
Đáp số : 24 học sinh
14 tháng 12 2017
Số học sinh giỏi toán của lớp đó là:
32:100x75=24 ( học sinh )
Đáp số : 24 học sinh
HN
2
P
16 tháng 9 2018
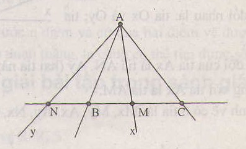
Xét ∆BDC có BE = ED (gt) và BM = MC (gt)
⇒⇒ ME là đường trung bình của ΔBDCΔBDC (dấu hiệu nhận biết đường trung bình của tam giác)
⇒⇒ EM // DC (tính chất đường trung bình của tam giác)
⇒⇒ DI // EM (Vì D, I, C thẳng hàng)
Xét ∆AEM có AD = DE và DI // EM (cmt) ⇒⇒ AI = IM (Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm của cạnh thứ ba
16 tháng 9 2018
ΔBDC có BE = ED và BM = MC
nên EM // DC suy ra DI // EM
ΔAEM có AD = DE và DI // EM nên AI = IM (đpcm).
Gọi độ dài cạnh lăng trụ là a
Trong mp (ABC), lấy D đối xứng B qua AC \(\Rightarrow ABCD\) là hình thoi
Trong mp (A'B'C') lấy D' đối xứng B' qua A'C' \(\Rightarrow A'B'C'D'\) là hình thoi
\(\Rightarrow A'BCD'\) là hình bình hành nên \(A'B||D'C\)
\(\Rightarrow\left(A'B,B'C\right)=\left(D'C,B'C\right)=\widehat{B'CD'}\) (nếu nó nhọn, và bằng góc bù với nó nếu nó tù)
\(D'C=A'B=\sqrt{A'A^2+AB^2}=a\sqrt{2}\)
\(B'C=\sqrt{B'B^2+BC^2}=a\sqrt{2}\)
\(B'D'=BD=2.\dfrac{a\sqrt{3}}{2}=a\sqrt{3}\)
Áp dụng định lý hàm cos:
\(cos\widehat{B'CD'}=\dfrac{B'C^2+D'C^2-B'D'^2}{2B'C.D'C}=\dfrac{1}{4}\)
\(\Rightarrow\left(A'B,B'C\right)\approx75^031'\)