Cho hình thang có 2 đáy ( AB với CD ) . Gọi K là trung điểm của BC , lấy A' và D' sao cho K là trung điểm của A'Dvà AD'. Hỏi tam giác AD và A'D' là hình gì ? Vì sao?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 12 2022
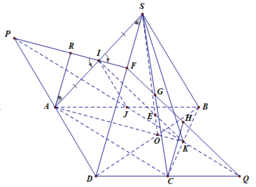
IJ là đường trung bình của hình thang \(\Rightarrow\left\{{}\begin{matrix}IJ||AB\\IJ=\dfrac{AB+CD}{2}\end{matrix}\right.\)
Qua G kẻ đường thẳng song song AB lần lượt cắt SB, SA tại E và F
\(\Rightarrow\) Tứ giác IJEF là thiết diện của (GIJ) và chóp
\(EF||AB||IJ\Rightarrow IJEF\) là hình thang
Gọi M là trung điểm AB
Theo tính chất trọng tâm và định lý Talet:
\(\dfrac{EF}{AB}=\dfrac{SG}{SM}=\dfrac{2}{3}\)
Để IJEF là hình bình hành \(\Leftrightarrow IJ=EF\)
\(\Leftrightarrow\dfrac{2}{3}AB=\dfrac{AB+CD}{2}\Leftrightarrow\dfrac{1}{3}AB=CD\)
\(\Rightarrow AB=3CD\)
18 tháng 1 2024
Xét hình thang ADCB có
Q,P lần lượt là trung điểm của AB,DC
=>QP là đường trung bình của hình thang ADCB
=>QP//AD//BC và \(QP=\dfrac{AD+BC}{2}=\dfrac{\dfrac{BC}{2}+BC}{2}=\dfrac{3}{4}BC\)
Ta có: M là trung điểm của BC
=>\(BM=MC=\dfrac{BC}{2}\)
Ta có: N là trung điểm của MC
=>\(MN=NC=\dfrac{MC}{2}=\dfrac{BC}{4}\)
BM+MN=BN
=>\(BN=\dfrac{1}{4}BC+\dfrac{1}{2}BC=\dfrac{3}{4}BC\)
=>QP=BN
Ta có: QP//BN
QP=BN
Do đó: \(\overrightarrow{QP}=\overrightarrow{BN}\)
=>Điểm E trùng với điểm P
12 tháng 7 2021
a) Xét ΔBDC có
K là trung điểm của BD(gt)
F là trung điểm của BC(gt)
Do đó: KF là đường trung bình của ΔBDC(Định nghĩa đường trung bình của tam giác)
Suy ra: KF//DC và \(KF=\dfrac{DC}{2}\)(Định lí 2 về đường trung bình của tam giác)
hay KF//AB
