Tính độ dài nhỏ nhất của cạnh Huyền trong các tam giác vuông có chu vi = k không thay đổi
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NM
Nguyễn Minh Quang
Giáo viên
7 tháng 1 2021
A B C M D E
dễ thấy tứ giác ADME là hình chữ nhật do có 3 góc vuông
nên chu vi ADME=2(AE+EM)
mà do ABC vuông cân nên góc ECM =45 độ nên MEC vuông cân tại E nên EM=EC
nên chu vi ADME=2(AE+EM)=2(AE+EC)=2AC là không đổi
b.DE=AM nhỏ nhaasrt khi M là hình chiếu của A lên BC
HQ
Hà Quang Minh
Giáo viên
26 tháng 9 2023
Đặt cạnh huyền của tam giác là x (\(x > 8\))
Theo giải thiết ta tính được cạnh góc vuông là \(x - 8\)
Áp dụng định lý Pitago ta tính được cạnh góc vuông còn lại là \(\sqrt {{x^2} - {{\left( {x - 8} \right)}^2}} = \sqrt {16x - 64} \)
Ta có chu vi của tam giác là \(x + \left( {x - 8} \right) + \sqrt {16x - 64} = 30\)
\(\begin{array}{l} \Leftrightarrow \sqrt {16x - 64} = 38 - 2x\\ \Rightarrow 16x - 64 = {\left( {38 - 2x} \right)^2}\\ \Rightarrow 16x - 64 = 1444 - 152x + 4{x^2}\\ \Rightarrow 4{x^2} - 168x + 1508 = 0\end{array}\)
\( \Rightarrow x = 13\) và \(x = 29\)
Thay \(x = 13\) và \(x = 29\) vào phương trình \(\sqrt {16x - 64} = 38 - 2x\) ta thấy chỉ có \(x = 13\) thảo mãn phương trình
Vậy cạnh huyền có độ dài là 13 cm.
CM
13 tháng 8 2018
Gọi độ dài các cạnh góc vuông của tam giác lần lượt là 5k và 12k với k> 0. Dùng định lý Py-ta-go tính được độ dài cạnh huyền là 13k, do đó
5k +12k + 13k = 30 => k = 1.
Từ đó độ dài cạnh huyền là 13 cm.
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
14 tháng 7 2023
Bài 8: Vì em nhắn tin nhờ cô giảng bài 8 nên cô chỉ giảng bài 8 thôi nhé
Gọi các cạnh góc vuông, cạnh huyền của tam giác cần tìm lần lượt là: a; b; c
Theo bài ra ta có: a+b+c =36; \(\dfrac{a}{b}\) = \(\dfrac{3}{4}\)
\(\dfrac{a}{b}\) = \(\dfrac{3}{4}\) ⇒ \(\dfrac{a}{3}\) = \(\dfrac{b}{4}\) ⇒ \(\dfrac{a^2}{9}\) = \(\dfrac{b^2}{16}\) = \(\dfrac{a^2+b^2}{9+16}\) (1)
Vì tam giác vuông nên ta theo pytago ta có: a2 + b2 = c2 (2)
Thay (2) vào (1) ta có: \(\dfrac{a^2}{9}\) = \(\dfrac{b^2}{16}\) = \(\dfrac{c^2}{25}\)
⇒ \(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}\) = \(\dfrac{a+b+c}{3+4+5}\) = \(\dfrac{36}{12}\) = 3
a = 3.3 = 9 (cm)
b = 3.4 = 12 (cm)
c = 3.5 = 15 (cm)
Kết luận: độ dài cạnh bé của góc vuông là: 9 cm
dộ dài cạnh lớn của góc vuông là 12 cm
độ dài cạnh huyền là 15 cm
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
14 tháng 7 2023
Bài 9:
a,Gọi độ dài cạnh góc vuông là: a
Theo pytago ta có: a2 + a2 = 22 = 4 ⇒ 2a2 = 4 ⇒ a2 = 2 ⇒ a = \(\sqrt{2}\)
b, Gọi độ dài cạnh góc vuông là :b
Theo pytago ta có:
b2 + b2 = 102 =100 ⇒ 2b2 = 100 ⇒ b2 = 50⇒ b = 5\(\sqrt{2}\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
14 tháng 7 2023
Bài 8 cô làm rồi nhé.
Bài 10 ; Gọi độ dài các cạnh góc của tam giác vuông lần lượt là:
a; b theo bài ra ta có:
\(\dfrac{a}{5}\) = \(\dfrac{b}{12}\) \(\Rightarrow\) \(\dfrac{a^2}{25}\) = \(\dfrac{b^2}{144}\) = \(\dfrac{a^2+b^2}{25+144}\) (1)
Theo pytago ta có: a2 + b2 = 522 = 2704 (2)
Thay (2) vào (1) ta có: \(\dfrac{a^2}{25}\) = \(\dfrac{b^2}{144}\) = \(\dfrac{2704}{169}\) = 16
⇒ a2 = 25.16 = (4.5)2 ⇒ a = 20
b2 = 144.16 = (12.4)2 ⇒ b = 48
QD
23 tháng 5 2016
Gọi độ dài 1 cạnh góc vuông là x (cm), x < 25
độ dài cạnh góc vuông còn lại là 60 - 25 - x = 35 - x (cm)
Theo đề bài ta có pt :
x + (35 - x ) = 25^2 (ĐL Pytago) <=> x^2 - 35x + 300 = 0
Δ = (−35)2 − 4.1.300 = 25
x = (35+5) : 2 = 20 ; x = 35 - 20 = 15
Vậy độ dài 2 góc vuông là 20cm và 15cm
BN
23 tháng 5 2016
Gọi độ dài 1 cạnh góc vuông là x (cm), x < 25
độ dài cạnh góc vuông còn lại là 60 - 25 - x = 35 - x (cm)
Theo đề bài ta có pt :
x2 + (35 - x2) = 25^2 (ĐL Pytago) <=> x^2 - 35x + 300 = 0
\(\Delta=\left(-35\right)^2-4.1.300=25\)
x1 = (35+5) : 2 = 20 ; x2 = 35 - 20 = 15
Vậy độ dài 2 góc vuông là 20cm và 15cm
PT
1
CM
28 tháng 7 2017
Gọi b, c là độ dài các cạnh góc vuông, a là độ dài cạnh huyền (tính bằng cm) ( 0 < b; c < a)
+) Do các cạnh góc vuông tỉ lệ với 7 và 24 nên:
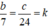⇒ b = 7k, c = 24k.
Theo định lý Py-ta-go:
a2 = b2 + c2 = (7k)2 + (24k)2 = 625k2 = (25k)2
Nên a = 25k.
Theo đề bài, chu vi tam giác bằng 112 cm nên: a + b + c = 112 (cm).
Suy ra: 25k + 7k + 24k = 112
Hay 56k = 112
Từ đó ta tính được k = 2. Vậy a = 50cm.
18 tháng 1 2022
tớ gợi ý nhé:
gọi hai cạnh góc vuông là a;b, cạnh huyền là c
đặt \(\dfrac{a}{8}\) = \(\dfrac{b}{15}\) vào k
=> a=....; b= .....
sau đó là áp dụng đl pi-ta-go( ghép hết vào với nhau),tính c
Thế là xong
Gọi \(c\) là cạnh huyền của tam giác vuông đó và \(a,b\) là 2 cạnh góc vuông. Khi đó: \(a+b+c=k\) và \(c^2=a^2+b^2\)
\(\Rightarrow c^2=\left(a+b\right)^2-2ab\ge\left(a+b\right)^2-2.\dfrac{\left(a+b\right)^2}{4}=\dfrac{\left(a+b\right)^2}{2}=\dfrac{\left(k-c\right)^2}{2}\)
\(\Leftrightarrow2c^2\ge k^2-2kc+c^2\)
\(\Leftrightarrow c^2+2kc-k^2\ge0\)
\(\Leftrightarrow\left(\dfrac{c}{k}\right)^2+2.\dfrac{c}{k}-1\ge0\)
\(\Leftrightarrow\dfrac{c}{k}\ge\sqrt{2}-1\) \(\Leftrightarrow c\ge\left(\sqrt{2}-1\right)k\)
Dấu "=" xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}c=\left(\sqrt{2}-1\right)k\\a=b=\dfrac{k-c}{2}=\dfrac{\left(2-\sqrt{2}\right)k}{2}\end{matrix}\right.\), thỏa mãn.
Vậy độ dài nhỏ nhất của cạnh huyền là \(\left(\sqrt{2}-1\right)k\)