Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Đồ thị hàm số y = ax + b đi qua A(1; 3) và B(-1; -1)
Vậy a = 2; b = 1; hàm số y = 2x + 1.
b) y = ax + b song song với y = x + 5
⇒ a = 1.
Đồ thị hàm số đi qua C(1; 2) ⇔ 2 = a.1 + b ⇔ a + b = 2 ⇒ b = 1.
Vậy a = 1; b = 1.
a) Đồ thị hàm số y = ax + b đi qua A(1; 3) và B(-1; -1)
Vậy a = 2; b = 1; hàm số y = 2x + 1.
b) y = ax + b song song với y = x + 5
⇒ a = 1.
Đồ thị hàm số đi qua C(1; 2) ⇔ 2 = a.1 + b ⇔ a + b = 2 ⇒ b = 1.
Vậy a = 1; b = 1.
1: Vì (d) đi qua A(-2;5) và B(1;-4) nên ta có hệ phương trình:
-2a+b=5 và a+b=-4
=>a=-3; b=-1
2:
a: Để hàm số đồng biến thì 2m-1>0
=>m>1/2
Đáp án B
Ta có g x = f x − x 2 2 → g ' x = f ' x − x ; ∀ x ∈ ℝ
Phương trình g ' x = 0 ⇔ f ' x = x . Dựa vào hình vẽ, ta thấy đồ thị hàm số y = f ' x cắt đường thẳng y = x tại ba điểm phân biệt x = − 2 ; x = 0 ; x = 1
Do đó, để phương trình g x = 0 có 4 nghiệm phân biệt ⇔ g 0 > 0 g 1 < 0 , g − 2 < 0
\(\lim\limits_{x\rightarrow0}\dfrac{\sqrt[3]{ax+1}-\sqrt[]{1-bx}}{x}=\lim\limits_{x\rightarrow0}\dfrac{\dfrac{ax}{\sqrt[3]{\left(ax+1\right)^2}+\sqrt[3]{ax+1}+1}+\dfrac{bx}{1+\sqrt[]{1-bx}}}{x}\)
\(=\lim\limits_{x\rightarrow0}\left(\dfrac{a}{\sqrt[3]{\left(ax+1\right)^2}+\sqrt[3]{ax+1}+1}+\dfrac{b}{1+\sqrt[]{1-bx}}\right)=\dfrac{a}{3}+\dfrac{b}{2}\)
Hàm liên tục tại \(x=0\) khi:
\(\dfrac{a}{3}+\dfrac{b}{2}=3a-5b-1\Leftrightarrow8a-11b=3\)
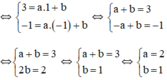
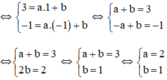
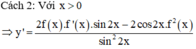
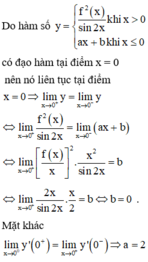
a: Vì hệ số góc là -4 nên a=-4
=>y=-4x+b
Thay x=2 và y=-5 vào y=-4x+b, ta được:
b-8=-5
=>b=3
Vậy: y=-4x+3
b: Vì đồ thị hàm số y=ax+b song song với đường thẳng y=2x-1
nên \(\left\{{}\begin{matrix}a=2\\b\ne-1\end{matrix}\right.\)
Vậy: y=2x+b(b\(\ne\)-1)
c: Thay x=0 và y=4 vào y=ax+b, ta được:
\(a\cdot0+b=4\)
=>b=4
=>y=ax+4
Thay x=4/5 và y=0 vào y=ax+4, ta được:
\(\dfrac{4}{5}a+4=0\)
=>\(\dfrac{4}{5}a=-4\)
=>a=-5
vậy: y=-5x+4
d: Vì đồ thị hàm số y=ax+b vuông góc với đường thẳng y=-2x+3 nên -2a=-1
=>\(a=\dfrac{1}{2}\)
Vậy: \(y=\dfrac{1}{2}x+b\)
Thay x=1/4 và y=-5 vào y=1/2x+b, ta được:
\(b+\dfrac{1}{2}\cdot\dfrac{1}{4}=-5\)
=>\(b=-5-\dfrac{1}{8}=-\dfrac{41}{8}\)