a.-0,25 + \(\dfrac{2}{3}\) b. \(1\dfrac{4}{23}\) + \(\dfrac{-5}{21}\) - \(\dfrac{4}{23}\) + 0,5 - \(\dfrac{16}{21}\)
c. 2 - [(1-\(\dfrac{1}{3}\))12 : (\(\dfrac{2}{3}\))10- \(1\dfrac{4}{9}\) -20240]
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Số lần so sánh giữa các phần tử: Trong thuật toán sắp xếp chọn, số lần so sánh giữa các phần tử là cố định, không phụ thuộc vào dữ liệu đầu vào. Cụ thể, số lần so sánh trong thuật toán sắp xếp chọn là \(\dfrac{n\left(n-1\right)}{2}\), với n là số phần tử trong mảng hoặc danh sách.
Số lần hoán đổi giữa các phần tử: Trong thuật toán sắp xếp chọn, số lần hoán đổi giữa các phần tử có thể đạt đến tối đa n-1 lần, với n là số phần tử trong mảng hoặc danh sách.
Vậy độ phức tạp thời gian của thuật toán sắp xếp chọn là O(n2), hay \(\dfrac{n\left(n-1\right)}{2}\) lần so sánh và tối đa n-1 lần hoán đổi giữa các phần tử.

Đánh giá được mức đơn giản của thuật toán, từ đó tìm ra được cách giải nhanh nhất.

tham khảo
/Em không đồng ý với ý kiến của Mai.Vì như vậy sẽ là gian lận trong học tập sẽ không giúp gì được cho mik mà làm mik ngày càng ỷ lại,không tốt cho tương lai của bản thân mik.
Em không đồng ý với ý kiến của Mai,vì Mai xui Hoa không cần suy nghĩ mà chỉ cần chép trong vở bài tập toán,nếu Lan chép sẽ không hiệu quả trong học tập.

tính E(300)=300/log2(300), E(90000)=90000/log2(90000)
Vì độ hiệu quả tỉ lệ thuận với thời gian thực hiện
nên ta có tỉ số 0,02/E(300)=x/E(90000) (x là giá trị cần tìm).
Từ đó tính được x=3

Hai tiêu chí đánh giá độ phức tạp tính toán quan trọng nhất là:
1. Thời gian thực thi (Runtime): Đây là thời gian mà chương trình hoặc thuật toán mất để thực hiện một nhiệm vụ hoặc tính toán. Thời gian thực thi là một tiêu chí quan trọng vì nó đo lường tốc độ hoạt động của chương trình, và đối với các ứng dụng yêu cầu xử lý dữ liệu lớn hoặc thực hiện tính toán phức tạp, thời gian thực thi càng nhanh thì chương trình càng hiệu quả.
2. Độ phức tạp không gian (Space complexity): Đây là lượng bộ nhớ mà chương trình hoặc thuật toán sử dụng trong quá trình thực hiện nhiệm vụ hoặc tính toán. Độ phức tạp không gian cũng là một tiêu chí quan trọng vì nó đo lường khả năng sử dụng tài nguyên bộ nhớ của chương trình, và đối với các ứng dụng có yêu cầu về tài nguyên hạn chế, độ phức tạp không gian càng thấp thì chương trình càng hiệu quả.
THAM KHẢO!
1. Tính số lần lặp của vòng lặp bên trong của thuật toán sắp xếp chèn tuyến tính.

2. Tính số lần lặp của vòng lặp ngoài của thuật toán sắp xếp chèn tuyến tính.
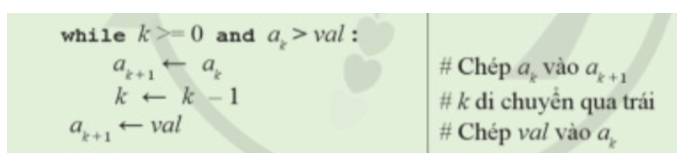
3. Ước lượng độ phức tạp thời gian của thuật toán sắp xếp chèn tuyến tính:
Vòng lặp for bên ngoài kiểm soát việc thực hiện đúng n-1 bước.
Vòng lặp while lồng bên trong thực hiện đồng thời cùng lúc hai việc a) và b) theo cách dịch chuyển dần từng bước sang trái, từ vị trí i tới vị trí k+1
\(a,-0,25+\dfrac{2}{3}=-\dfrac{3}{4}+\dfrac{2}{3}=-\dfrac{9}{12}+\dfrac{8}{12}=-\dfrac{1}{12}\\ b,1\dfrac{4}{23}+\dfrac{-5}{21}-\dfrac{4}{23}+0,5-\dfrac{16}{21}\\ =\left(\dfrac{27}{23}-\dfrac{4}{23}\right)+\left(-\dfrac{5}{21}-\dfrac{16}{21}\right)+0,5\\ =\dfrac{23}{23}-\dfrac{21}{21}+0,5\\ =1-1+0,5\\ =0,5\\ c,2-\left[\left(1-\dfrac{1}{3}\right)^{12}:\left(\dfrac{2}{3}\right)^{10}-1\dfrac{4}{9}-2024^0\right]\\ =2-\left[\left(\dfrac{2}{3}\right)^{12}:\left(\dfrac{2}{3}\right)^{10}-\dfrac{13}{9}-1\right]\\ =2-\left[\dfrac{4}{9}-\dfrac{13}{9}-\dfrac{9}{9}\right]\\ =2-\left(-2\right)\\ =4\)
\(a,-0,25+\dfrac{2}{3}\\ =-\dfrac{1}{4}+\dfrac{2}{3}\\ =\dfrac{-3}{12}+\dfrac{8}{12}\\ =\dfrac{5}{12}\\ b,1\dfrac{4}{23}+\dfrac{-5}{21}-\dfrac{4}{23}+0,5-\dfrac{16}{21}\\ =1+\left(\dfrac{4}{23}-\dfrac{4}{23}\right)+\left(\dfrac{-5}{21}-\dfrac{16}{21}\right)+\dfrac{1}{2}\\ =1+\dfrac{-21}{21}+\dfrac{1}{2}\\ =1-1+\dfrac{1}{2}\\ =\dfrac{1}{2}\\ c,2-\left[\left(1-\dfrac{1}{3}\right)^{12}:\left(\dfrac{2}{3}\right)^{10}-1\dfrac{4}{9}-2024^0\right]\\ =2-\left[\left(\dfrac{2}{3}\right)^{12}:\left(\dfrac{2}{3}\right)^{10}-1-\dfrac{4}{9}-1\right]\\ =2-\left[\left(\dfrac{2}{3}\right)^2-2-\dfrac{4}{9}\right]\\ =2-\left(\dfrac{4}{9}-2-\dfrac{4}{9}\right)\\ =2+2\\ =4\)