Tìm x :
(x-40)²-48=-12
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
a) Thay m=3 vào (1), ta được:
\(x^2-4x+3=0\)
a=1; b=-4; c=3
Vì a+b+c=0 nên phương trình có hai nghiệm phân biệt là:
\(x_1=1;x_2=\dfrac{c}{a}=\dfrac{3}{1}=3\)
Bài 2:
a) Thay m=0 vào (2), ta được:
\(x^2-2x+1=0\)
\(\Leftrightarrow\left(x-1\right)^2=0\)
hay x=1


Gọi x1,x2 là các nghiệm của phương trình đã cho
Áp dụng hệ thức Vi-et,ta có :
x1 + x2 = -5 ; x1x2 = -1
gọi y1,y2 là các nghiệm của phương trình phải lập,ta được :
y1 + y2 = x14 + x24 , y1y2 = x14x24
Ta có : x12 + x22 = ( x1 + x2 )2 - 2x1x2 = 25 + 2 - 27
Do đó : y1 + y2 = x14 + x24 = ( x12 + x22 )2 - 2x12x22 = 729 - 2 = 727
y1y2 = ( x1x2 )4 = 1
Từ đó pt phải lập có dạng : y2 - 727y + 1 = 0
Ta co: P = -1 <0
=> (1) có 2 nghiệm phân biệt khác dấu
Gọi hai nghiệm đó là \(x_1;x_2\)
=> \(x_1+x_2=-5;x_1.x_2=-1\)
Ta có: \(\left(x_1.x_2\right)^4=\left(-1\right)^4=1\)
\(\left(x_1\right)^4+\left(x_2\right)^4=\left(x_1^2+x_2^2\right)^2-2x_1^2x_2^2=\left[\left(x_1+x_2\right)^2-2x_1x_2\right]^2-2x_1^2x_2^2\)
\(=\left[\left(-5\right)^2-2.\left(-1\right)\right]^2-2.\left(-1\right)^2\)
\(=727\)
=> Phương trình có các nghiệm lũy thừa bậc 4 của các nghiệm phương trình (1) là:
\(x^2-727x+1=0\)

a) Tam thức bậc hai \(f\left( x \right) = 2{x^2} - 15x + 28\) có hai nghiệm phân biệt là \({x_1} = \frac{7}{2};{x_2} = 4\)
và có \(a = 2 > 0\) nên \(f\left( x \right) \ge 0\) khi x thuộc hai nửa khoảng \(\left( { - \infty ;\frac{7}{2}} \right];\left[ {4; + \infty } \right)\)
Vậy tập nghiệm của bất phương trình \(2{x^2} - 15x + 28 \ge 0\) là \(\left( { - \infty ;\frac{7}{2}} \right] \cup \left[ {4; + \infty } \right)\)
b) Tam thức bậc hai \(f\left( x \right) = - 2{x^2} + 19x + 255\) có hai nghiệm phân biệt là \({x_1} = - \frac{{15}}{2};{x_2} = 17\)
và có \(a = - 2 < 0\) nên \(f\left( x \right) > 0\) khi x thuộc khoảng \(\left( { - \frac{{15}}{2};17} \right)\)
Vậy tập nghiệm của bất phương trình \( - 2{x^2} + 19x + 255 > 0\) là \(\left( { - \frac{{15}}{2};17} \right)\)
c) \(12{x^2} < 12x - 8 \Leftrightarrow 12{x^2} - 12x + 8 < 0\)
Tam thức bậc hai \(f\left( x \right) = 12{x^2} - 12x + 8\) có \(\Delta = - 240 < 0\) và \(a = 12 > 0\)
nên \(f\left( x \right) = 12{x^2} - 12x + 8\) dương với mọi x
Vậy bất phương trình \(12{x^2} < 12x - 8\) vô nghiệm
d) \({x^2} + x - 1 \ge 5{x^2} - 3x \Leftrightarrow -4{x^2} + 4x - 1 \ge 0\)
Tam thức bậc hai \(f\left( x \right) = -4{x^2} + 4x - 1\) có \(\Delta = 4^2 - 4.(-4).(-1)\)
Do đó tam thức bậc hai có nghiệm kép \({x_1} = {x_2}= \frac{1}{2}\) và a = - 4 < 0
Vậy bất phương trình \({x^2} + x - 1 \ge 5{x^2} - 3x\) có tập nghiệm S = {\(\frac{1}{2}\)}

Phương trình bậc hai 6x2 + x + 5 = 0
Có a = 6; b = 1; c = 5; Δ = b2 – 4ac = 12 – 4.5.6 = -119 < 0
Vậy phương trình vô nghiệm.

Phương trình bậc hai 6x2 + x – 5 = 0
Có a = 6; b = 1; c = -5; Δ = b2 – 4ac = 12 – 4.6.(-5) = 121 > 0
Áp dụng công thức nghiệm, phương trình có hai nghiệm phân biệt là:
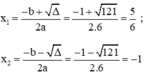
Vậy phương trình có hai nghiệm là -1 và 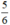
\(\left(x-40\right)^2-48=-12\\ =>\left(x-40\right)^2=-12+48\\ =>\left(x-40\right)^2=36\\ =>\left(x-40\right)^2=6^2\\ TH1:x-40=6\\ =>x=6+40\\ =>x=46\\ TH2:x-40=-6\\ =>x=40-6\\ =>x=34\)
Vậy: ...
\(\left(x-40\right)^2-48=-12\)
\(\left(x-40\right)^2=\left(-12\right)+48\)
\(\left(x-40\right)^2=36\)
\(\left(x-40\right)^2=6^2\)
\(x-40=6\)
\(x=6+40\)
\(x=46\)