vận dụng hằng đẳng thức để giải phương trình:
e,x2- 10x - 11 = 0
giúp e vs ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
17 tháng 2 2022
\(\left(4A\right)\\ a,\\ \Leftrightarrow\left[\left(x-2\right)\left(2x+3\right)\right]\left[\left(x-2\right)\left(2x+3\right)\right]=0\\ \Leftrightarrow\left(-x-5\right)\left(3x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}-x-5=0\\3x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-5\\x=\dfrac{-1}{3}\end{matrix}\right.\\ b,\\ \Leftrightarrow\left[3\left(2x+1\right)\right]^2-\left[2\left(x+1\right)\right]^2=0\\ \Leftrightarrow\left[3\left(2x+1\right)-2\left(x+1\right)\right]\left[3\left(2x+1\right)+2\left(x+1\right)\right]=0\\ \Leftrightarrow\left(4x+1\right)\left(8x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}4x+1=0\\8x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-1}{4}\\x=\dfrac{-5}{8}\end{matrix}\right.\\ c,\\ \Leftrightarrow\left[\left(x+1\right)+1\right]^2=0\\ \Leftrightarrow\left(x+1\right)+1=0\\ \Leftrightarrow x+2=0\Rightarrow x=-2\\ d,\\ \Leftrightarrow\left(x-1\right)\left(x-3\right)\left(x+3\right)+\left(x+3\right)=0\\ \Leftrightarrow\left(x+3\right)\left[\left(x-1\right)\left(x+3\right)+1\right]=0\\ \Leftrightarrow\left(x+3\right)\left(x^2-4x+4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x+3=0\\\left(x+2\right)^2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=-2\end{matrix}\right.\)
\(\left(4B\right)\\ a,\\ \Leftrightarrow49-14x+x^2-4\left(x+25\right)^2=0\\ \Leftrightarrow49-14x+x^2-4x^2-40x-100=0\\ \Leftrightarrow3x^2-54x-51=0\\ \Leftrightarrow-3\left(x^2+18x+17\right)=0\\ \Leftrightarrow\left(x+1\right)\left(x+17\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x+1=0\\x+17=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=-17\end{matrix}\right.\\ b,\\ \Leftrightarrow4x^2\left(x^2-2x+1\right)-\left(4x^2+4x+1\right)=0\\ \Leftrightarrow x^2-6x=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x-6=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=6\end{matrix}\right.\)
\(c,\\ \Leftrightarrow\left(x+1\right)\left(x^2-x+1\right)=\left(x+1\right)\left(2-x\right)=0\\ \Leftrightarrow\left(x+1\right)\left[\left(x^2-x+1\right)-\left(2-x\right)\right]=0\\ \Leftrightarrow\left(x+1\right)\left(x^1-1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x+1=0\\x-1=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=1\\x=-1\end{matrix}\right.\\ d,\\ \Leftrightarrow\left(x-5\right)\left(x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x-5=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\\x=-1\end{matrix}\right.\)
MH
1
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
14 tháng 8 2023
Phương trình bậc hai có dạng: a\(x^2\) + b\(x\) + c
Bước 1: Đưa nó về bình phương của một tổng hoặc một hiệu cộng với một số nào đó. nếu a > 0 thì em sẽ tìm giá trị nhỏ nhất; nếu a < 0 thì em sẽ tìm giá trị lớn nhất
Bước 2: lập luận chỉ ra giá trị lớn nhất hoặc nhỏ nhất
Bước 3: kết luận
Giải:
A = 3\(x^2\) - 5\(x\) + 3 Vì a = 3 > 0 vậy biểu thức A chỉ tồn tại giá trị nhỏ nhất
A = 3\(x^2\) - 5\(x\) + 3
A = 3.(\(x\)2 - 2.\(x\).\(\dfrac{5}{6}\) + \(\dfrac{25}{36}\)) + \(\dfrac{11}{12}\)
A = 3.(\(x\) - \(\dfrac{5}{6}\))2 + \(\dfrac{11}{12}\)
Vì (\(x-\dfrac{5}{6}\))2 ≥ 0 ⇒ 3.(\(x\) - \(\dfrac{5}{6}\))2 ≥ 0 ⇒ 3.(\(x-\dfrac{5}{6}\))2 + \(\dfrac{11}{12}\) ≥ \(\dfrac{11}{12}\)
Amin = \(\dfrac{11}{12}\) ⇔ \(x\) = \(\dfrac{5}{6}\)
PC
18 tháng 9 2017
Nhìn cái HD là ra đề bài đề bắt rút gọn BT đó ba =)))ngonhuminh
TV
1
9 tháng 9 2017
A.Lý thuyết về dấu tam thức bậc hai
1. Tam thức bậc hai (một ẩn) là đa thức có dạng f(x) = ax2 + bx + c trong đó x là biến a, b, c là các số đã cho, với a ≠ 0.
Định lí. Cho tam thức bậc hai f(x) = ax2 + bx + c (a ≠ 0)
có biệt thức ∆ = b2 – 4ac.
- Nếu ∆ < 0 thì với mọi x, f(x) có cùng dấu với hệ số a.
- Nếu ∆ = 0 thì f(x) có nghiệm kép x = , với mọi x ≠
, f(x) có cùng dấu với hệ số a.
- Nếu ∆ > 0, f(x) có 2 nghiệm x1, x2 (x1 < x2) và luôn cùng dấu với hệ số a với mọi x ngoài đoạn [x1; x2] và luôn trái dấu với hệ số a với mọi x trong đoạn (x1; x2).
2. Bất phương trình bậc hai một ẩn.
Là mệnh đề chứa một biến có một trong các dạng:
ax2 + bx + c > 0, ax2 + bx + c < 0, ax2 + bx + c ≥ 0, ax2 + bx + c ≤ 0 trong đó vế trái là một tam thức bậc hai.
Để giải bất phương trình bậc hai một ẩn ta dùng định lí về dấu của tam thức bậc hai.
22 tháng 6 2017
Ta có:
\(\sqrt{3x^2+6x+12}+\sqrt{5x^4-10x^2+9}\)
\(=\sqrt{\left(3x^2+6x+3\right)+9}+\sqrt{\left(5x^4-10x^2+5\right)+4}\)
\(=\sqrt{3\left(x+1\right)^2+9}+\sqrt{5\left(x^2-1\right)^2+4}\ge3+2=5\left(1\right)\)
Ta lại có:
\(-2x^2-4x+3=-2\left(x+1\right)^2+5\le5\left(2\right)\)
Từ (1) và (2) dấu = xảy ra khi \(x=-1\)
CM
6 tháng 4 2017
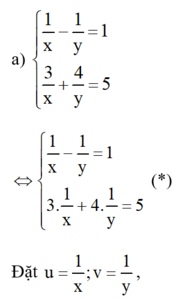
hệ phương trình (*) trở thành :
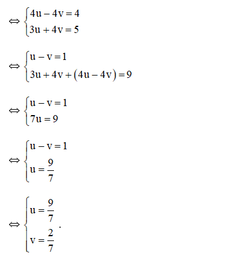
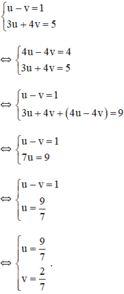
+ u = 9 7 ⇒ 1 x = 9 7 ⇒ x = 7 9 + v = 2 7 ⇒ 1 y − 2 7 ⇒ y − 7 2
Vậy hệ phương trình có nghiệm (7/9;7/2)
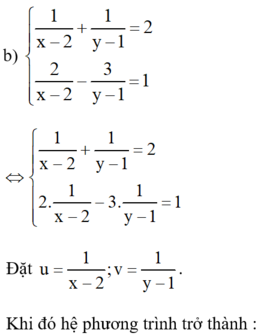
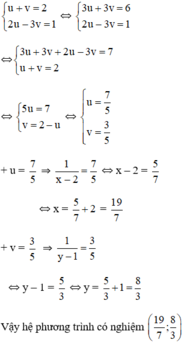
Kiến thức áp dụng
Giải hệ phương trình bằng phương pháp cộng đại số
1) Nhân hai vế của phương trình với mỗi hệ số thích hợp (nếu cần) sao cho hệ số của một trong hai ẩn bằng nhau hoặc đối nhau.
2) Áp dụng quy tắc cộng đại số để được hệ phương trình mới, trong đó có một phương trình mà hệ số của một trong hai ẩn bằng 0 (tức là phương trình một ẩn).
3) Giải phương trình một ẩn vừa thu được rồi suy ra nghiệm của hệ đã cho và kết luận.
28 tháng 6 2018
\(\sqrt{x+2\sqrt{x-1}}=2\)
\(\Leftrightarrow\sqrt{\left(\sqrt{x-1}\right)^2+2\sqrt{x-1}+1}=2\)
\(\Leftrightarrow\sqrt{\left(\sqrt{x-1}+1\right)^2}=2\)
\(\Leftrightarrow\left|\sqrt{x-1}+1\right|=2\)
\(\Leftrightarrow\orbr{\begin{cases}\sqrt{x-1}+1=2\\\sqrt{x-1}+1=-2\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}\sqrt{x-1}=1\Leftrightarrow x-1=1\Leftrightarrow x=2\\\sqrt{x-1}=-3\left(vl\right)\end{cases}}\)
Vậy phương trình có tập nghiệm \(S=\left\{2\right\}\)
\(x^2-10x-11=0\)
=>\(x^2-10x+25-36=0\)
=>\(\left(x-5\right)^2-6^2=0\)
=>(x-5-6)(x-5+6)=0
=>(x-11)(x+1)=0
=>\(\left[{}\begin{matrix}x-11=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=11\\x=-1\end{matrix}\right.\)
\(x^2\)\(-2.x.5+5^2\)\(-36\)\(=0\)
\(\Leftrightarrow\)\(\left(x-5\right)^2\)\(-36=0\)
\(\Leftrightarrow\left(x-5^{ }\right)^2\)\(=36\)
\(\Leftrightarrow\left[{}\begin{matrix}x-5=6\\x-5=-6\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=11\\x=-1\end{matrix}\right.\)