Rút gọn các phân thức sau
\(\dfrac{x+2\sqrt{x}+1}{x+3\sqrt{x}+2}\) với \(x\ge0\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Qui tắc rút gọn một phân thức đại số.
- Phân tích tử và mẫu thành nhân tử (nếu cần) để tìm nhân tử chung.
- Chia cả tử và mẫu cho nhân tử chung đó.
Rút gọn:
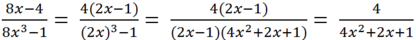

a) Thay phân thức P vào biểu thức A rồi rút gọn chúng ta thu được A = u + v với điều kiện các biểu thức có nghĩa.
b) Tương tự a) ta có B = 1.

\(\dfrac{10x^5y^2-30x^2y^6}{20x^2y^2}=\dfrac{10x^2y^2\left(x^3-3y^3\right)}{20x^2y^2}=\dfrac{x^3-3y^3}{2}\)
\(\dfrac{10x^5y^2-30x^2y^6}{20x^2y^2}=\dfrac{10x^2y^2\left(x^3-3y^4\right)}{10x^2y^2.2}=\dfrac{x^3-3y^4}{2}\)

\(c,=\dfrac{x\left(x-y\right)}{5y\left(y-x\right)}=\dfrac{-x}{5y}\\ d,=\dfrac{x\left(x-y\right)-\left(x-y\right)}{x\left(x+y\right)-\left(x+y\right)}=\dfrac{\left(x-1\right)\left(x-y\right)}{\left(x-1\right)\left(x+y\right)}=\dfrac{x-y}{x+y}\)

\(\dfrac{x^2+x-2}{x^2+7x+10}=\dfrac{\left(x-1\right)\left(x+2\right)}{\left(x+2\right)\left(x+5\right)}=\dfrac{x-1}{x+5}\)
\(=\dfrac{\left(x-1\right)\left(x+2\right)}{\left(x+2\right)\left(x+5\right)}=\dfrac{x-1}{x+5}\)


\(=\dfrac{-3x\left(x-y\right)}{6y\left(y-x\right)}=\dfrac{-3x\left(x-y\right)}{-6y\left(x-y\right)}=\dfrac{x}{2y}\)

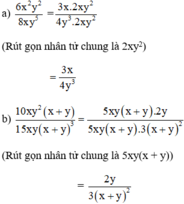
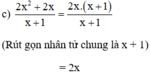
Phân tích tử số thành nhân tử :
x2 – xy – x + y = (x2 – xy) – (x – y) = x.(x – y) – (x – y) = (x – 1)(x – y)
+ Phân tích mẫu số thành nhân tử :
x2 + xy – x – y = (x2 + xy) – (x + y) = x(x + y) – (x + y) = (x – 1)(x + y)
Do đó ta có :
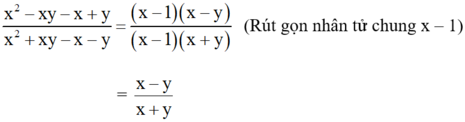
\(=\dfrac{\left(\sqrt{x}+1\right)^2}{\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}+2}\)