Cho hình bình hành ABCD có E là trung điểm AD, F là trung điểm BC.
a) CMR: BE= DF
b) Gọi O là trung điểm EF. CMR: EF,DB,AC đồng quy
c) AC cắt BE, DF lần lượt tại I và K. CMR: DI // BK và AI = IK = CK
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔSAC có
H,K lần lượt là trung điểm của SA,SC
=>HK là đường trung bình
=>HK//AC
Xét (GHK) và (ABCD) có
HK//AC
\(G\in\left(GHK\right)\cap\left(ABCD\right)\)
Do đó: (GHK) giao (ABCD)=xy, xy đi qua G và xy//HK//AC
b: Chọn mp(SBD) có chứa SD
Gọi O là giao điểm của AC và BD
ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
Xét ΔABC có
G là trọng tâm
BO là trung tuyến của ΔABC
Do đó: B,O,G thẳng hàng
=>G\(\in\)BD
Trong mp(SAC), gọi I là giao điểm của SO với HK
\(I\in SO\subset\left(SBD\right);I\in HK\subset\left(GHK\right)\)
=>\(I\in\left(SBD\right)\cap\left(GHK\right)\)(1)
\(G\in BD\subset\left(SBD\right);G\in\left(GHK\right)\)
=>\(G\in\left(SBD\right)\cap\left(GHK\right)\left(2\right)\)
Từ (1) và (2) suy ra \(\left(SBD\right)\cap\left(GHK\right)=GI\)
Gọi M là giao điểm của SD với GI
=>M là giao điểm của SD với (SHK)
c: Xét ΔSAC có
O,K lần lượt là trung điểm của CA,CS
=>OK là đường trung bình của ΔSAC
=>OK//SA và OK=SA/2
OK=SA/2
SH=SA/2
Do đó: OK=SH
Xét tứ giác SHOK có
SH//OK
SH=OK
Do đó: SHOK là hình bình hành
=>HK cắt SO tại trung điểm của mỗi đường
mà E là trung điểm của HK
nên Elà trung điểm của SO
=>E trùng với I
=>(SBD) giao (GHK)=GE
=>G,E,M thẳng hàng

Cạnh AB = DC 3,3 cm . Cạnh AD = BC 2,6 cm
S hình bình hành ABCD là : 2,6 x 3,3 = 8,58 cm\(^2\)
QM = PN = 2,3 cm , MN = QP = 1,8 cm
Diện tích các phần ko tô màu là : [1,35 x 2,3 + 1,8 x 1,35 + 1,35 x 1,65 + 1,65 x 1,35] : 2 = 4,995 cm\(^2\)
Diện tích hình tứ giác là : 8,58 - 4,995 = 3,585 cm\(^2\)
Tỉ số % của diện tích hình tứ giác MNPQ và diện tích hình bình hành ABCD là :
3,585 : 8,58 x 100 = 41,873%

Đáp án A
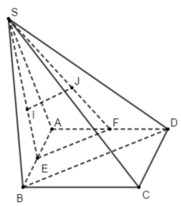
Tam giác SAB có I là trọng tâm và E là trung điểm của AB
Nên ta có S I S E = 2 3 (1)
Tam giác SAD có J là trọng tâm và F là trung điểm của AD
Nên ta có S J S F = 2 3 (2)
Từ (1) và (2) ta có: IJ // EF (3) (định lý Ta-lét trong tam giác SEF)
Tam giác ABD có EF là đường trung bình nên EF // BD (4)
Từ (3) và (4) suy ra IJ // BD
Mà BD (SBD)
Do đó IJ // (SBD).

a: Gọi O là giao điểm của AC và BD
\(O\in AC\subset\left(SAC\right);O\in BD\subset\left(SBD\right)\)
=>\(O\in\left(SAC\right)\cap\left(SBD\right)\)
mà \(S\in\left(SAC\right)\cap\left(SBD\right)\)
nên \(\left(SAC\right)\cap\left(SBD\right)=SO\)
b: Xét (SAD) và (SBC) có
AD//BC
\(S\in\left(SAD\right)\cap\left(SBC\right)\)
Do đó: (SAD) giao (SBC)=xy, xy đi qua S và xy//AD//BC
d: Trong mp(SAB), gọi I là giao điểm của AB với SM
\(I\in SM;I\in AB\subset\left(ABCD\right)\)
Do đó: I là giao điểm của SM với mp(ABCD)

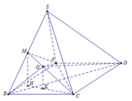
Đáp án A
Gọi H và K lần lượt là hình chiếu của M và G xuống ABCD
Ta có V V ' = 1 3 M H . S A B C 1 3 G K . S A D B = 3 2 . 1 2 S A B C D 1 2 S A B C D = 3 2

a: Gọi O là giao điểm của AC và BD
ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
Xét ΔABD có
AO,DM là các đường trung tuyến
AO cắt DM tại G
Do đó: G là trọng tâm của ΔABD
b: Xét ΔABD có
AO là đường trung tuyến
G là trọng tâm
Do đó: \(AG=\dfrac{2}{3}\cdot AO=\dfrac{2}{3}\cdot\dfrac{1}{2}\cdot AC=\dfrac{1}{3}AC\)
Ta có: CG+GA=CA
=>\(GA+\dfrac{1}{3}AC=AC\)
=>\(GA=\dfrac{2}{3}AC\)
\(\dfrac{AG}{GA}=\dfrac{\dfrac{1}{3}AC}{\dfrac{2}{3}AC}=\dfrac{1}{3}:\dfrac{2}{3}=\dfrac{1}{2}\)
=>GA=2AG
a: Ta có: \(BF=FC=\dfrac{BC}{2}\)
\(AE=ED=\dfrac{AD}{2}\)
mà BC=AD
nên BF=FC=AE=ED
Xét tứ giác BFDE có
BF//DE
BF=DE
Do đó: BFDE là hình bình hành
=>EB=DF(3)
b: Ta có: BFDE là hình bình hành
=>BD cắt FE tại trung điểm của mỗi đường
mà O là trung điểm của FE
nên O là trung điểm của BD
Ta có: ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
mà O là trung điểm của BD
nên O là trung điểm của AC
=>AC,BD,EF đồng quy tại O
c: Xét ΔABD có
BE,AO là các đường trung tuyến
BE cắt AO tại I
Do đó: I là trọng tâm của ΔABD
=>\(BI=\dfrac{2}{3}BE\left(1\right)\)
Xét ΔDBC có
DF,CO là các đường trung tuyến
DF cắt CO tại K
Do đó: K là trọng tâm của ΔDBC
=>\(DK=\dfrac{2}{3}DF\left(2\right)\)
Từ (1),(2),(3) suy ra BI=DK
Xét tứ giác BIDK có
BI//DK
BI=DK
Do đó: BIDK là hình bình hành
=>BK=DI
Xét ΔBCI có
F là trung điểm của CB
FK//BI
Do đó: K là trung điểm của CI
=>CK=KI
Xét ΔAKD có
E là trung điểm của AD
EI//KD
Do đó: I là trung điểm của AK
=>AI=IK
Do đó: AI=IK=KC