C1: Chóp SABCD có M thuộc AB, N thuộc tam giác SCD. Tìm g/điểm của MN với mp (SAC)
C2: Chóp SABC có M,N,P,Q là trung điểm SB, SC ,SA,BC. Tìm g/điểm G của PQ với (AMN) và tính tỉ số của GP/GQ.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
12 tháng 7 2017
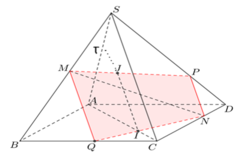
+) Qua N kẻ NP// SC .
- Ta có: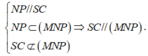 
- Từ đó ta có: (MNP) là mặt phẳng qua MN và song song với SC.
- Vậy (P) ≡ (MNP).
+) Ta có: (P) ∩ (SCD) = NP.
- Ta có: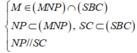 
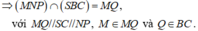
+) Trong (ABCD), gọi I = NQ ∩ AC.
- Ta có: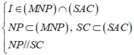 
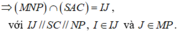
30 tháng 10 2023
a: Xét ΔSBD có
M,N lần lượt là trung điểm của SB,SD
=>MN là đường trung bình
=>MN//BD
BD//MN
\(MN\subset\left(AMN\right)\)
BD không thuộc mp(AMN)
Do đó: BD//(AMN)
b: Gọi O là giao điểm của AC và BD
\(O\in AC\subset\left(SAC\right)\)
\(O\in BD\subset\left(SBD\right)\)
Do đó: \(O\in\left(SAC\right)\cap\left(SBD\right)\)
mà \(S\in\left(SAC\right)\cap\left(SBD\right)\)
nên \(\left(SAC\right)\cap\left(SBD\right)=SO\)
Chọn mp(SBD) có chứa MN
(SBD) giao (SAC)=SO(cmt)
Gọi K là giao điểm của SO với MN
=>K là giao điểm của MN với mp(SAC)
CM
8 tháng 9 2019
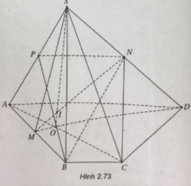
(h.2.73) a) Gọi O = AC ∩ MD Trong mặt phẳng (SMB) gọi I = SO ∩ MN.
Ta có: I = (SAC) ∩ MN
b) AD // BC (BC ⊂ (SBC))
⇒ AD // (SBC). Mặt phẳng (SAD) cắt mặt phẳng (NBC) theo giao tuyến NP // AD (P ∈ SA). Ta có thiết diện cần tìm là hình thang BCNP.
CM
2 tháng 8 2019
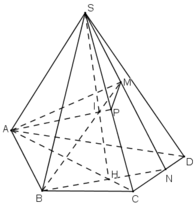
a) SM, CD cùng thuộc (SCD) và không song song.
Gọi N là giao điểm của SM và CD.
⇒ N ∈ CD và N ∈ SM
Mà SM ⊂ (SMB)
⇒ N ∈ (SMB)
⇒ N = (SMB) ∩ CD.
b) N ∈ CD ⊂ (ABCD)
⇒ BN ⊂ (ABCD)
⇒ AC; BN cùng nằm trong (ABCD) và không song song
Gọi giao điểm của AC và BN là H.
+ H ∈ AC ⊂ (SAC)
+ H ∈ BN ⊂ (SBM)
⇒ H ∈ (SAC) ∩ (SBM)
Dễ dàng nhận thấy giao điểm thứ hai của (SAC) và (SBM) là S
⇒ (SAC) ∩ (SBM) = SH.
c) Trong mp(SBM), gọi giao điểm của BM và SH là I, ta có:
I ∈ BM
I ∈ SH ⊂ (SAC).
⇒ I = BM ∩ (SAC).
) Trong mp(SAC), gọi giao điểm của AI và SC là P.
+ P ∈ AI, mà AI ⊂ (AMB) ⇒ P ∈ (AMB)
⇒ P = (AMB) ∩ SC.
Lại có P ∈ SC, mà SC ⊂ (SCD) ⇒ P ∈ (SCD).
⇒ P ∈ (AMB) ∩ (SCD).
Lại có: M ∈ (SCD) (gt)
⇒ M ∈ (MAB) ∩ (SCD)
Vậy giao điểm của (MAB) và (SCD) là đường thẳng MP.
Q
31 tháng 3 2017
a) Trong (SCD) kéo dài SM cắt CD tại N, Chứng minh N thuộc (SBM)
b) (SBM) ≡ (SBN). Giao tuyến cần tìm là SO
c) Trong (SBN) ta có MB giao SO tại I
d) Trong (ABCD) , ta có AB giao CD tại K, Trong (SCD), ta có KQ giao SC tại P
Từ đó suy ra được giao tuyến của hai mặt phẳng (SCD) và (ABM) là KQ.
Câu 2;
Chọn mp(SAQ) có chứa PQ
Trong mp(ABC), gọi I là giao điểm của SQ và MN
I∈SQ⊂(SAQ)
I∈MN⊂(AMN)
Do đó: I∈(SAQ) giao (AMN)(1)
A∈(SAQ)
A∈(AMN)
Do đó: A∈(SAQ) giao (AMN)(2)
từ (1),(2) suy ra (SAQ) giao (AMN)=AI
Gọi G là giao điểm của PQ và AI
=>G là giao điểm của PQ và mp(AMN)
Xét ΔBSC có
M,Q lần lượt là trung điểm của BS,BC
=>MQ là đường trung bình của ΔBSC
=>MQ//SC và \(MQ=\frac{SC}{2}\)
\(MQ=\frac{SC}{2}\)
\(SN=\frac{SC}{2}\)
Do đó: MQ=SN
Xét tứ giác SMQN có
SN//QM
SN=QM
Do đó: SMQN là hình bình hành
=>SQ cắt MN tại trung điểm của mỗi đường
=>I là trung điểm chung của SQ và MN
Xét ΔSAQ có
AI,QP là các đường trung tuyến
AI cắt QP tại G
Do đó:G là trọng tâm của ΔSAQ
=>\(\frac{GP}{GQ}=\frac12\)
Câu 1: Trong mp(SCD), gọi K là giao điểm của SN và CD
Chọn mp(SMK) có chứa MN
Trong mp(ABCD), gọi I là giao điểm của MK và AC
I∈MK⊂(SMK)
I∈AC⊂(SAC)
Do đó: I∈(SMK) giao (SAC)(1)
ta có: S∈(SMK)
S∈(SAC)
Do đó; S∈(SMK) giao (SAC)(2)
Từ (1),(2) suy ra (SMK) giao (SAC)=SI
Gọi X là giao điểm của SI và MN
=>X là giao điểm của MN và mp(SAC)