(x-5).(x-7)=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
18 tháng 2 2017
(x – 1)(x – 3)(x + 5)(x + 7) = 0
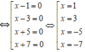
Vậy tập nghiệm của phương trình là S = { -7;-5;1;3}
2
11 tháng 1 2023
Bài `1:`
`h)(3/4x-1)(5/3x+2)=0`
`=>[(3/4x-1=0),(5/3x+2=0):}=>[(x=4/3),(x=-6/5):}`
______________
Bài `2:`
`b)3x-15=2x(x-5)`
`<=>3(x-5)-2x(x-5)=0`
`<=>(x-5)(3-2x)=0<=>[(x=5),(x=3/2):}`
`d)x(x+6)-7x-42=0`
`<=>x(x+6)-7(x+6)=0`
`<=>(x+6)(x-7)=0<=>[(x=-6),(x=7):}`
`f)x^3-2x^2-(x-2)=0`
`<=>x^2(x-2)-(x-2)=0`
`<=>(x-2)(x^2-1)=0<=>[(x=2),(x^2=1<=>x=+-2):}`
`h)(3x-1)(6x+1)=(x+7)(3x-1)`
`<=>18x^2+3x-6x-1=3x^2-x+21x-7`
`<=>15x^2-23x+6=0<=>15x^2-5x-18x+6=0`
`<=>(3x-1)(5x-1)=0<=>[(x=1/3),(x=1/5):}`
`j)(2x-5)^2-(x+2)^2=0`
`<=>(2x-5-x-2)(2x-5+x+2)=0`
`<=>(x-7)(3x-3)=0<=>[(x=7),(x=1):}`
`w)x^2-x-12=0`
`<=>x^2-4x+3x-12=0`
`<=>(x-4)(x+3)=0<=>[(x=4),(x=-3):}`
2
11 tháng 1 2023
`m)(1-x)(5x+3)=(3x-7)(x-1)`
`<=>(1-x)(5x+3)+(1-x)(3x-7)=0`
`<=>(1-x)(5x+3+3x-7)=0`
`<=>(1-x)(8x-4)=0<=>[(x=1),(x=1/2):}`
`p)(2x-1)^2-4=0`
`<=>(2x-1-2)(2x-1+2)=0`
`<=>(2x-3)(2x+1)=0<=>[(x=3/2),(x=-1/2):}`
`r)(2x-1)^2=49`
`<=>(2x-1-7)(2x-1+7)=0`
`<=>(2x-8)(2x+6)=0<=>[(x=4),(x=-3):}`
`t)(5x-3)^2-(4x-7)^2=0`
`<=>(5x-3-4x+7)(5x-3+4x-7)=0`
`<=>(x+4)(9x-10)=0<=>[(x=-4),(x=10/9):}`
`u)x^2-10x+16=0`
`<=>x^2-8x-2x+16=0`
`<=>(x-2)(x-8)=0<=>[(x=2),(x=8):}`
KT
2
25 tháng 10 2023
Để giải phương trình 2x - 7√x^2 + 5 = 0, ta có thể thực hiện các bước sau:
1. Đặt y = √x, ta có y^2 = x.
2. Thay thế x bằng y^2 trong phương trình ban đầu, ta được: 2y^2 - 7y + 5 = 0.
3. Giải phương trình bậc hai 2y^2 - 7y + 5 = 0 bằng cách sử dụng phương trình bậc hai thông thường hoặc sử dụng công thức Viết.
4. Giải phương trình bậc hai, ta có hai giá trị của y: y1 và y2.
5. Thay y1 và y2 vào phương trình y = √x, ta có hai giá trị của x: x1 = y1^2 và x2 = y2^2.
Vậy, để giải phương trình 2x - 7√x^2 + 5 = 0, ta cần giải phương trình bậc hai 2y^2 - 7y + 5 = 0 và sau đó tìm giá trị của x từ giá trị của y....
25 tháng 10 2023
\(2x-7\sqrt{x}+5=0\)(ĐKXĐ: x>=0)
=>\(2x-2\sqrt{x}-5\sqrt{x}+5=0\)
=>\(\left(\sqrt{x}-1\right)\left(2\sqrt{x}-5\right)=0\)
=>\(\left[{}\begin{matrix}\sqrt{x}-1=0\\2\sqrt{x}-5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}=1\\\sqrt{x}=\dfrac{5}{2}\end{matrix}\right.\)
=>x=1 hoặc x=25/4
LA
29 tháng 3 2022
1. 3x( x - 2 ) - ( x - 2 ) = 0
<=> ( x-2).(3x-1) = 0 => x = 2 hoặc x = \(\dfrac{1}{3}\)
2. x( x-1 ) ( x2 + x + 1 ) - 4( x - 1 )
<=> ( x - 1 ).( x (x^2 + x + 1 ) - 4 ) = 0
(phần này tui giải được x = 1 thôi còn bên kia giải ko ra nha )
3 \(\left\{{}\begin{matrix}\sqrt{5}x-2y=7\\\sqrt{5}x-5y=10\end{matrix}\right.\)<=> \(\left\{{}\begin{matrix}y=-1\\x=\sqrt{5}\end{matrix}\right.\)
AH
29 tháng 3 2022
\(1. 3x^2 - 7x +2=0\)
=>\(Δ=(-7)^2 - 4.3.2\)
\(= 49-24 = 25\)
Vì 25>0 suy ra phương trình có 2 nghiệm phân biệt:
\(x_1\)=\(\dfrac{-\left(-7\right)+\sqrt{25}}{2.3}=\dfrac{7+5}{6}=2\)
\(x_2\)=\(\dfrac{-\left(-7\right)-\sqrt{25}}{2.3}=\dfrac{7-5}{6}=\dfrac{1}{3}\)
Y
12 tháng 4 2022
\(a,\dfrac{x-3}{x}=\dfrac{x-3}{x+3}\)\(\left(đk:x\ne0,-3\right)\)
\(\Leftrightarrow\dfrac{x-3}{x}-\dfrac{x-3}{x+3}=0\)
\(\Leftrightarrow\dfrac{\left(x-3\right)\left(x+3\right)-x\left(x-3\right)}{x\left(x+3\right)}=0\)
\(\Leftrightarrow x^2-9-x^2+3x=0\)
\(\Leftrightarrow3x-9=0\)
\(\Leftrightarrow3x=9\)
\(\Leftrightarrow x=3\left(n\right)\)
Vậy \(S=\left\{3\right\}\)
Y
12 tháng 4 2022
\(b,\dfrac{4x-3}{4}>\dfrac{3x-5}{3}-\dfrac{2x-7}{12}\)
\(\Leftrightarrow\dfrac{4x-3}{4}-\dfrac{3x-5}{3}+\dfrac{2x-7}{12}>0\)
\(\Leftrightarrow\dfrac{3\left(4x-3\right)-4\left(3x-5\right)+2x-7}{12}>0\)
\(\Leftrightarrow12x-9-12x+20+2x-7>0\)
\(\Leftrightarrow2x+4>0\)
\(\Leftrightarrow2x>-4\)
\(\Leftrightarrow x>-2\)
PT
1
CM
17 tháng 3 2018
(2x + 7)(x – 5)(5x + 1) = 0
⇔ 2x + 7 = 0 hoặc x – 5 = 0 hoặc 5x + 1 = 0
+ 2x + 7 = 0 ⇔ 2x = -7 ⇔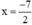 
+ x – 5 = 0 ⇔ x = 5.
+ 5x + 1 = 0 ⇔ 5x = -1 ⇔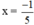 
Vậy phương trình có tập nghiệm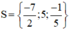 
15 tháng 7 2023
1) \(\sqrt[]{3x+7}-5< 0\)
\(\Leftrightarrow\sqrt[]{3x+7}< 5\)
\(\Leftrightarrow3x+7\ge0\cap3x+7< 25\)
\(\Leftrightarrow x\ge-\dfrac{7}{3}\cap x< 6\)
\(\Leftrightarrow-\dfrac{7}{3}\le x< 6\)
H
23 tháng 2 2023
`a,x^2 +4x-5=0`
`<=> x^2-x+5x-5=0`
`<=> x(x-1)+5(x-1)=0`
`<=>(x-1)(x+5)=0`
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\x+5=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-5\end{matrix}\right.\)
`b, x^2 -x-12=0`
`<=> x^2 +3x-4x-12=0`
`<=>(x^2+3x)-(4x+12)=0`
`<=>x(x+3)-4(x+3)=0`
`<=>(x+3)(x-4)=0`
\(\Leftrightarrow\left[{}\begin{matrix}x+3=0\\x-4=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=4\end{matrix}\right.\)
`c, (2x-7)^2 - 6(2x-7)(x-3)=0`
`<=>(2x-7)(2x-7 -6x+18)=0`
`<=>(2x-7) ( -4x+11)=0`
\(\Leftrightarrow\left[{}\begin{matrix}2x-7=0\\-4x+11=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=7\\-4x=-11\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{7}{2}\\x=\dfrac{11}{4}\end{matrix}\right.\)
23 tháng 2 2023
a: =>(x+5)(x-1)=0
=>x=1 hoặc x=-5
b: =>(x-4)(x+3)=0
=>x=4 hoặc x=-3
c: =>(2x-7)(2x-7-6x+18)=0
=>(2x-7)(-4x+11)=0
=>x=11/4 hoặc x=7/2
Q
5
2
12 tháng 5 2022
`3x+7=0`
`<=>3x=-7`
`<=>x=-7/3`
Vậy `S={-7/3}`
______________________
`2x(x-2)+2x(5-3x)=0`
`<=>2x(x-2+5-3x)=0`
`<=>2x(3-2x)=0`
`@TH1:2x=0<=>x=0`
`@TH2: 3-2x=0<=>2x=3<=>x=3/2`
Vậy `S={0;3/2}`
TC
12 tháng 5 2022
3x+7=0
\(\Leftrightarrow3x=-7\Leftrightarrow x=-\dfrac{7}{3}\)
2x(x-2)+2x(5-3x)=0
\(\Leftrightarrow2x\left(x-2+5-3x\right)=0\)
\(\Leftrightarrow2x\left(-2x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=0\\-2x=-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{-3}{-2}=\dfrac{3}{2}\end{matrix}\right.\)
`(x-5)(x-7) = 0`
`<=> x-5 = 0` hoặc `x - 7 = 0`
`<=> x = 5` hoặc `x = 7`
Vậy ` x = 5` hoặc `x = 7`
(x-5)(x-7)=0
=>\(\left[{}\begin{matrix}x-5=0\\x-7=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\\x=7\end{matrix}\right.\)