Cho hình vuông ABCD có cạnh a, M là một điểm trên đường thẳng BC ( M khác B, C). Vẽ hình vuông AMEN. Tia AM cắt DC tại Q, tia NA cắt CB tại P. Gọi I là trung điểm của PQ, CMR: N,D,C thẳng hàng; tam giác APQ vuông cân
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tự vẽ hình nhé
Tạo hình: lấy điểm T thuộc đường thẳng DC( T không nằm trên đọan DC) sao cho góc DAT = góc BAM
lấy điểm H thuộc đường thẳng BC( H không nằm trên đọan BC) sao cho góc BAH = góc DAN.
Bạn tự c/m: \(\hept{\begin{cases}\Delta ATD=\Delta AMB\\\Delta ADN=\Delta ABH\end{cases}\Rightarrow\hept{\begin{cases}AT=AM\\AN=AH\end{cases}}}\) ( 2 cạnh tương ứng )
Tiếp theo c/m \(\hept{\begin{cases}\Delta TAN=\Delta MAN\\\Delta MAN=\Delta MAH\end{cases}\Rightarrow\hept{\begin{cases}\widehat{TNA}=\widehat{MNA}\\\widehat{NMA}=\widehat{HMA}\end{cases}}}\)( 2 góc tương ứng )
Đến đây bạn tự làm nốt nhé

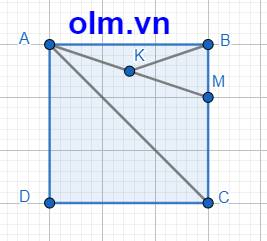
SABCD = 12 \(\times\)12 = 144 (cm2)
SABC = 12 \(\times\) 12 : 2 = 72 (cm2)
BM = 12 \(\times\) \(\dfrac{2}{3}\) = 8 (cm)
CM = 12 - 8 = 4 (cm)
SACM = 12 \(\times\)4 : 2 = 24 (cm2)
b, SABK = \(\dfrac{1}{2}\)SABM (vì hai tam giác có chung đường cao hạ từ đỉnh B xuống đáy BM và AK = \(\dfrac{1}{2}\)AM)
SABM = SABC - SAMC = 72 - 24 = 48 (cm2)
SABK = 48 : 2 = 24 (cm2)
Đáp số: a, SABCD = 144 cm2; SACM = 24 cm2
b, SABK = 24 cm2