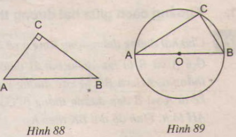
Chứng minh rằng: nếu tam giác ABC vuông tại C thì điểm C thuộc đường tròn có bán bán kính là AB.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Đúng
Gọi O là trung điểm của AB.
Ta có CO là trung tuyến ứng với cạnh huyền nên
⇒ OC = AB/2 = OA = OB.
⇒ A, B, C cùng thuộc đường tròn bán kính OA.
Tâm O là trung điểm của AB nên AB là đường kính.
Vậy C thuộc đường tròn đường kính AB.
b) Đúng
Gọi O là tâm đường tròn.
⇒ OA = OB = OC = R
AB là đường kính nên AB = 2R.
Tam giác ABC có CO là trung tuyến và CO = AB/2
⇒ ΔABC vuông tại C.


Vì tam giác ABC vuông tại A nên tâm đường tròn ngoại tiếp tam giác ABC là trung điểm của cạnh huyền BC.
Ta có: BC = 2R
Giả sử đường tròn (O) tiếp với AB tại D, AC tại E và BC tại F
Theo kết quả câu a) bài 58, ta có ADOE là hình vuông.
Suy ra: AD = AE = EO = OD = r
Theo tính chất hai tiếp tuyến cắt nhau ta có:
AD = AE
BD = BF
CE = CF
Ta có: 2R + 2r = BF + FC + AD + AE
= (BD + AD) + (AE + CE)
= AB + AC
Vậy AB = AC = 2(R + r)

a: ΔABC vuông tại A
mà AM là đường trung tuyến
nên MA=MB=MC
=>ΔABC nội tiếp (M)
b: ΔABC vuông tại A
=>\(BC^2=AB^2+AC^2\)
=>\(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
ΔABC vuông tại A có AM là đường trung tuyến
nên \(AM=\dfrac{BC}{2}=5\left(cm\right)\)
=>R=5cm

a:\(BC=\sqrt{4^2+3^2}=5\left(cm\right)\)
AH=4*3/5=2,4cm
b: ΔCAD cân tại C
mà CH là đường cao
nên CH là phân giác của góc ACD
Xét ΔCAB và ΔCDB có
CA=CD
góc ACB=góc DCB
CB chung
Do dó: ΔCAB=ΔCDB
=>góc CDB=90 độ
=>BD là tiếp tuyến của (C)

a:
góc ABA'=góc ACA'=1/2*180=90 độ
Xét ΔBOA' có
BH vừa là đường cao, vừa là trung tuyến
=>ΔBOA' cân tại B
mà OB=OA'
nên ΔBOA' đều
=>góc A'BH=30 độ
=>góc ABC=60 độ
Xét ΔACB có
AH vừa là đường cao, vừa là trung tuyến
góc ABC=60 độ
=>ΔACb đều
b: ΔOBA' đều có BH là đường cao
nên BH=OA'*căn 3/2=R*căn 3/2
=>CH=R*căn 3/2
=>BC=R*căn 3
=>DC=căn DB^2-BC^2=R
DH=căn DC^2+CH^2=R*căn 7/2