4x=3y và x2=288
chỉ mình với
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
8 tháng 12 2018
Đáp án D
Phương pháp:
(P) // (α) => Phương trình mặt phẳng (P) có dạng 4x + 3y - 12z + D = 0 (D ≠ 0)
(P) tiếp xúc với (S) => d(I;(P)) = R với I; R là tâm và bán kính mặt cầu (S)
Cách giải:
Gọi mặt phẳng (P) là mặt phẳng cần tìm
(P) // (α) Phương trình mặt phẳng (P) có dạng 4x + 3y - 12z + D = 0 (D ≠ 0)
Mặt cầu (S) có tâm I (1;2;3), bán kính R = 4
(P) tiếp xúc với (S) => d(I;(P)) = R
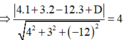
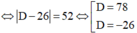
Vậy mặt phẳng (P) thỏa mãn yêu cầu bài toán có phương trình
CM
27 tháng 8 2018
Đáp án D
Phương pháp:
(P)// α => Phương trình mặt phẳng (P) có dạng 4x+3y-12z+D=0 (D khác 10)
(P) tiếp xúc với (S) => d(I;(P))= R với I; R là tâm và bán kính mặt cầu (S) .
Cách giải:
Gọi mặt phẳng là mặt phẳng cần tìm.
(P)// α =>Phương trình mặt phẳng có dạng 4x+3y-12z+D=0 (D khác 10)
Mặt cầu (S) có tâm I(1;2;3), bán kính R=4
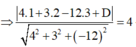
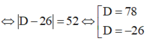
Vậy mặt phẳng (P) thỏa mãn yêu cầu bài toán có phương trình
4 tháng 12 2021
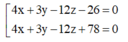
a)\(y=x^2-4x+3=\left(x-3\right)\left(x-1\right)\)
b)\(y=x^2+4x+3=\left(x+1\right)\left(x+3\right)\)
c)\(y=-x^2+4x-3=\left(x-3\right)\left(x-1\right)\)
d)\(y=-x^2-4x-3=\left(x+1\right)\left(x+3\right)\)
H9
HT.Phong (9A5)
CTVHS
29 tháng 9 2023
a) \(\dfrac{1}{x^3-8}=\dfrac{1}{\left(x-2\right)\left(x^2+2x+4\right)}=\dfrac{2}{2\left(x-2\right)\left(x^2+2x+4\right)}\)
\(\dfrac{3}{4-2x}=\dfrac{-3}{2\left(x-2\right)}=\dfrac{-3\left(x^2+2x+4\right)}{2\left(x-2\right)\left(x^2+2x+4\right)}\)
b) \(\dfrac{x}{x^2-1}=\dfrac{x}{\left(x+1\right)\left(x-1\right)}=\dfrac{x\left(x+1\right)}{\left(x+1\right)^2\left(x-1\right)}\)
\(\dfrac{1}{x^2+2x+1}=\dfrac{1}{\left(x+1\right)^2}=\dfrac{x-1}{\left(x+1\right)^2\left(x-1\right)}\)
c) \(\dfrac{1}{x+2}=\dfrac{\left(x-2\right)^2}{\left(x+2\right)\left(x-2\right)^2}\)
\(\dfrac{1}{x^2-4x+4}=\dfrac{1}{\left(x-2\right)^2}=\dfrac{x+2}{\left(x+2\right)\left(x-2\right)^2}\)
\(\dfrac{5}{2-x}=\dfrac{-5}{x-2}=\dfrac{-5\left(x+2\right)\left(x-2\right)}{\left(x+2\right)\left(x-2\right)^2}\)
d) \(\dfrac{1}{3x+3y}=\dfrac{1}{3\left(x+y\right)}=\dfrac{\left(x-y\right)^2}{3\left(x+y\right)\left(x-y\right)^2}\)
\(\dfrac{2x}{x^2-y^2}=\dfrac{2x}{\left(x+y\right)\left(x-y\right)}=\dfrac{6x\left(x-y\right)}{3\left(x+y\right)\left(x-y\right)^2}\)
\(\dfrac{x^2-xy+y^2}{x^2-2xy+y^2}=\dfrac{x^2-xy+y^2}{\left(x-y\right)^2}=\dfrac{3\left(x^2-xy+y^2\right)\left(x+y\right)}{3\left(x+y\right)\left(x-y\right)^2}=\dfrac{3\left(x^3+y^3\right)}{3\left(x+y\right)\left(x-y\right)^2}\)
14 tháng 11 2021
\(a,=x\left(x+y\right)+5\left(x+y\right)=\left(x+5\right)\left(x+y\right)\\ b,=x\left(y-x\right)-3\left(y-x\right)=\left(x-3\right)\left(y-x\right)\\ c,=18x-4x^3=2x\left(9-2x^2\right)\\ d,=\left(x-2\right)^2-4y^2=\left(x-2y-2\right)\left(x+2y-2\right)\\ e,=x^2-x-9x+9=\left(x-1\right)\left(x-9\right)\\ f,=4x^2-6x+2x-3=\left(2x-3\right)\left(2x+1\right)\)
22 tháng 10 2021
3: \(x^3+3x^2-16x-48\)
\(=x^2\left(x+3\right)-16\left(x+3\right)\)
\(=\left(x+3\right)\left(x-4\right)\left(x+4\right)\)
CM
12 tháng 1 2018
Đường tròn (C) có tâm và bán kính là I(0; 0) và R= 3.
∆ tiếp xúc ( C ) => d( I ; ∆) = R => m 5 = 3 => m = 15 m = - 15
Chọn D.
CM
3 tháng 9 2017
(C): x 2 + y 2 − 4 x + 2 y − 15 = 0 và đường thẳng ∆: - 4x + 3y + 1 = 0.
Đường tròn (C): x 2 + y 2 − 4 x + 2 y − 15 = 0 có tâm I(2; -1) và bán kính R = 20 .
Khoảng cách d I , ∆ = − 4.2 + 3. − 1 + 1 5 = 2 < R nên đường thẳng cắt đường tròn tại hai điểm phân biệt A, B cách nhau một khoảng là
A B = 2 R 2 − d I , ∆ 2 = 8 .
ĐÁP ÁN C
Tìm x,y hả bạn
288 hay 289