vẽ hai góc kề bù xOy , yOx' , biết góc yOx = 120 độ . gọi Oz là tia phân giác của góc xOy , Oz' là tia phân giác của góc yOx' . tính zOy ,yOz' ,zOz'
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PA
30 tháng 7 2016
Bạn tự vẽ hình nha ==''
xOy + yOx' = 1800 (2 góc kề bù)
1200 + yOx' = 1800
yOx' = 1800 - 1200
yOx' = 600
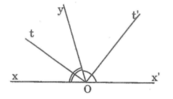
Ot là tia phân giác của xOy
=> xOt = tOy = xOy : 2 = 120 : 2 = 600
NH
2
KK
6 tháng 2 2019
O x z y
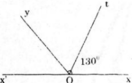
Giải : Ta có : \(\widehat{xOy}+\widehat{yOz}=180^0\)(kề bù)
=> góc yOz = 1800 - góc xOy
=> góc yOz = 1800 - 1300
=> góc yOz = 500
Vậy ...
6 tháng 2 2019
x O x' y 130 o ?
Vì 2 góc xOy và yOx' là 2 góc kề bù nên :
\(\widehat{xOy}+\widehat{yOx'}=180^0\)
\(130^0+\widehat{yOx'}=180^0\)
\(\widehat{yOx'}=180^0-130^0=50^0\).
PA
2
NQ
9 tháng 4 2021
Ta có yOx' = 180o-110o=70o
Ot là phân giác của xOy =>tOy=xOt=1/2xOy=110o:2=55o
Mà x'Ot=x'Oy+tOy
=>x'Ot=55o+70o=125o
26 tháng 4 2021
y t x x'
Vì Ot là tia phân giác\(\widehat{xOy}\) của nên \(\widehat{xOt}\)=\(\widehat{yOt}\)=\(\frac{\widehat{xOy}}{2}\)= 55
Vì \(\widehat{xOy}\)và \(\widehat{yOx'}\)là hai góc kề bù nên \(\widehat{xOy}\)+\(\widehat{yOx'}\)=180
110 + \(\widehat{yOx'}\)=180
\(\widehat{yOx'}\)=70
Ta có: \(\widehat{yOx'}\)+ \(\widehat{yOt}\)= \(\widehat{x'Ot}\)
70 + 55 =\(\widehat{x'Ot}\)
\(\widehat{x'Ot}\)= 125
TT
4
9 tháng 4 2021
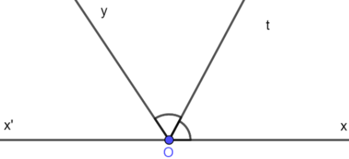
Ta có: tia Ot là tia phân giác của \(\widehat{xOy}\)
nên \(\widehat{xOt}=\dfrac{\widehat{xOy}}{2}=\dfrac{100^0}{2}=50^0\)
Ta có: \(\widehat{xOt}+\widehat{x'Ot}=180^0\)(hai góc kề bù)
\(\Leftrightarrow\widehat{x'Ot}+50^0=180^0\)
hay \(\widehat{x'Ot}=130^0\)
Vậy: \(\widehat{x'Ot}=130^0\)
9 tháng 4 2021
Ta có: \(\widehat{xOy}+\widehat{x'Oy}=180^0\)(hai góc kề bù)
\(\Leftrightarrow\widehat{x'Oy}+100^0=180^0\)
hay \(\widehat{x'Oy}=80^0\)
Ta có: tia Ot' là tia phân giác của \(\widehat{x'Oy}\)
nên \(\widehat{x'Ot'}=\dfrac{\widehat{x'Oy}}{2}=\dfrac{80^0}{2}=40^0\)
Ta có: \(\widehat{xOt'}+\widehat{x'Ot'}=180^0\)(hai góc kề bù)
\(\Leftrightarrow\widehat{xOt'}+40^0=180^0\)
hay \(\widehat{xOt'}=140^0\)
Vậy: \(\widehat{xOt'}=140^0\)
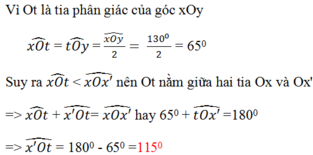
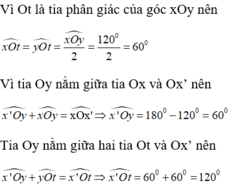
Ta có: \(\widehat{zOy}=\dfrac{1}{2}.\widehat{xOy}=\dfrac{1}{2}.120\text{°}=60\text{°}\)
\(\widehat{z'Oy}=\dfrac{1}{2}.\widehat{x'Oy}=\dfrac{1}{2}.\left(180\text{°}-\widehat{xOy}\right)=\dfrac{1}{2}.\left(180\text{°}-120\text{°}\right)=\dfrac{1}{2}.60\text{°}=30\text{°}\)
\(\widehat{zOz'}=\widehat{zOy}+\widehat{z'Oy}=60\text{°}+30\text{°}=90\text{°}\)