Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


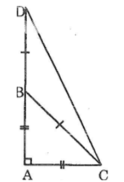
Ta có: ∆ABC vuông cân tại A
Suy ra: ∠ACB=∠ABC=45o
Lại có: ∆BCD vuông cân tại B (BC = BD)
Suy ra: ∠BCD=∠Dtính chất tam giác cân)
Trong ∆BCD ta có ∠ABC góc ngoài tại đỉnh B
Do vậy: ∠ABC=∠BCD + ∠D (tính chất góc ngoài của tam giác)
Suy ra: ∠ABC= ∠2∠BCD
Do đó: ∠BCD = 1/2 . ∠ABC = 1/2. 45º= 22º30’
=> ∠ACD = ∠ACB + ∠BCD = 45o+22o30'=67o30'


Gọi tứ giác nằm ngang là ABCD.
Hình dựng đứng là ABEMN
Từ điểm M kẻ đường thẳng//AB cắt BE tại G.
Do NM_|_AN tại A
MN//AB; BG//AN
=>BG_|_BE nên tam giác MGE vuông tại G. (1)
=>Tứ giác ABGN là hình chữ nhật=Hình chữ nhật ABCD( vì AB//=CD=14,2 m)
=>AN=AC=5 (m)
Từ (1) =>EG là đường cao của tam giác MGE có cạnh đáy MG.
=>EG=BE-BG=8-5=3 (m)
=>MG=NG-MN=14,2-6,2=8 (m)
Vậy S(MGE)=1/2.EG.MG=1/2.3.8=12 (m2)
=>S(ABCD)+S(ABGN)=2. S(ABCD)
=2.AB.AD=2.5.14,2=142 (m2)
=> Diện tích hình đã cho bằng:
12+142=154 m2
Đ s:
Gọi tứ giác nằm ngang là ABCD.
Hình dựng đứng là ABEMN
Từ điểm M kẻ đường thẳng//AB cắt BE tại G.
Do NM_|_AN tại A
MN//AB; BG//AN
=>BG_|_BE nên tam giác MGE vuông tại G. (1)
=>Tứ giác ABGN là hình chữ nhật=Hình chữ nhật ABCD( vì AB//=CD=14,2 m)
=>AN=AC=5 (m)
Từ (1) =>EG là đường cao của tam giác MGE có cạnh đáy MG.
=>EG=BE-BG=8-5=3 (m)
=>MG=NG-MN=14,2-6,2=8 (m)
Vậy S(MGE)=1/2.EG.MG=1/2.3.8=12 (m2)
=>S(ABCD)+S(ABGN)=2. S(ABCD)
=2.AB.AD=2.5.14,2=142 (m2)
=> Diện tích hình đã cho bằng:
12+142=154 m2

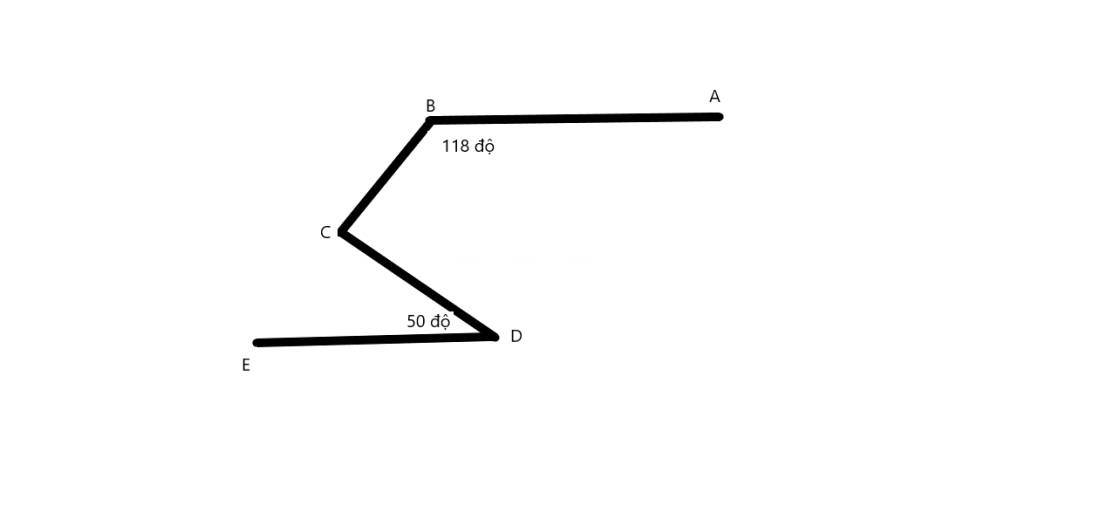
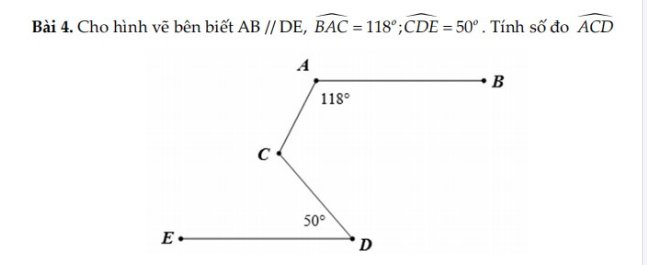
Kẻ Cx//AB//DE
Cx//AB
=>góc xCB+góc B=180 độ(trong cùng phía)
=>góc xCB=180-118=62 độ
Cx//DE
=>góc xCD=góc EDC(so le trong)
=>góc xCD=50 độ
góc BCD=62+50=112 độ
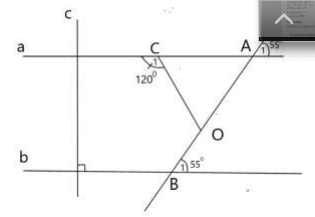 đây bạn ơi giúp mik nha
đây bạn ơi giúp mik nha