biểu thức (y+1) + (y+4) + (y+7)+...+(y+31) + (y+34) = 222
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
Y
21 tháng 2 2023
\(a,\dfrac{y-1}{y-2}-\dfrac{y+3}{y-4}=\dfrac{-2}{\left(y-2\right)\left(y-4\right)}\)
\(\Leftrightarrow\dfrac{\left(y-1\right)\left(y-4\right)-\left(y+3\right)\left(y-2\right)+2}{\left(y-2\right)\left(y-4\right)}=0\)\(\left(dkxd:y\ne4;2\right)\)
\(\Leftrightarrow y^2-4y-y+4-y^2+2y-3y+6+2=0\)
\(\Leftrightarrow-6y+12=0\)
\(\Leftrightarrow y=2\)\(\left(ktm\right)\)
Vậy ko có bất kì giá trị y nào để 2 biểu thức bằng nhau
\(b,\dfrac{8y}{y-7}+\dfrac{1}{7-y}=8\)
\(\Leftrightarrow\dfrac{8y}{y-7}-\dfrac{1}{y-7}=8\)\(\left(dkxd:y\ne7\right)\)
\(\Leftrightarrow8y-1-8\left(y-7\right)=0\)
\(\Leftrightarrow8y-1-8y+56=0\)(Vô lý)
Vậy ko có bất kì giá trị y nào để biểu thức có giá trị = 8
HQ
Hà Quang Minh
Giáo viên
17 tháng 9 2023
a)
\(\begin{array}{l}P(y) = - 12{y^4} + 5{y^4} + 13{y^3} - 6{y^3} + y - 1 + 9 = ( - 12 + 5){y^4} + (13 - 6){y^3} + y + ( - 1 + 9)\\ = - 7{y^4} + 7{y^3} + y + 8\end{array}\)
\(\begin{array}{l}Q(y) = - 20{y^3} + 31{y^3} + 6y - 8y + y - 7 + 11 = ( - 20 + 31){y^3} + (6 - 8 + 1)y + ( - 7 + 11)\\ = 11{y^3} - y + 4\end{array}\)
b)
Đa thức P(y): bậc của đa thức là 4; hệ số cao nhất là – 7; hệ số tự do là 8.
Đa thức Q(y): bậc của đa thức là 3; hệ số cao nhất là 11; hệ số tự do là 4.
TN
19 tháng 5 2018
\(x+y+z=2\sqrt{x-34}+4\sqrt{y-21}+6\sqrt{z-4}+45\)
ĐK: \(x\ge34;y\ge21;z\ge4\)
\(pt\Leftrightarrow x-34-2\sqrt{x-34}+1+y-21-4\sqrt{y-21}+4+z-4-6\sqrt{z-4}+9=0\)
\(\Leftrightarrow\left(\sqrt{x-34}-1\right)^2+\left(\sqrt{y-21}-2\right)^2+\left(\sqrt{z-4}-3\right)^2=0\left(1\right)\)
Dễ Thấy: \(VT_{\left(1\right)}\ge0\) nên dấu "=" khi
\(\hept{\begin{cases}\sqrt{x-34}=1\\\sqrt{y-21}=2\\\sqrt{z-4}=3\end{cases}}\)
Giải tiếp rồi thay vào T
LT
7 tháng 6 2020
b) \(\frac{8-y}{y-7}+\frac{1}{7-y}=8\)
ĐKXĐ: \(x\ne7\)
\(\Leftrightarrow\frac{\left(8-y\right)\left(7-y\right)}{\left(y-7\right)\left(7-y\right)}+\frac{y-7}{\left(y-7\right)\left(7-y\right)}=\frac{8\left(y-7\right)\left(7-y\right)}{\left(y-7\right)\left(7-y\right)}\)
\(\Rightarrow56-15y+y^2+y-7=112y-8y^2-392\)
\(\Leftrightarrow49-14y+y^2=112y-8y^2-392\)
\(\Leftrightarrow9y^2-126y+441=0\)
\(\Leftrightarrow9\left(y^2-14y+49\right)=0\)
\(\Leftrightarrow\left(y-7\right)^2=0\)
\(\Leftrightarrow y-7=0\)
\(\Leftrightarrow y=7\left(Loại\right)\)
Vậy không có giá trị nào để biểu thức \(\frac{8-y}{y-7}+\frac{1}{7-y}\) có giá trị bằng 8.
LT
7 tháng 6 2020
a) \(\frac{y-1}{y-2}-\frac{y+3}{y-4}=\frac{-2}{\left(y-2\right)\left(y-4\right)}\)
ĐKXĐ: \(y\ne2;y\ne4\)
\(\Leftrightarrow\frac{\left(y-1\right)\left(y-4\right)}{\left(y-2\right)\left(y-4\right)}-\frac{\left(y+3\right)\left(y-2\right)}{\left(y-2\right)\left(y-4\right)}=\frac{-2}{\left(y-2\right)\left(y-4\right)}\)
\(\Rightarrow y^2-5y+4-y^2-y+6=-2\)
\(\Leftrightarrow10-6y=-2\)
\(\Leftrightarrow-6y=-12\)
\(\Leftrightarrow y=2\left(Loại\right)\)
Vậy không có giá trị nào của y để biểu thức \(\frac{y-1}{y-2}-\frac{y+3}{y-4}\) và \(\frac{-2}{\left(y-2\right)\left(y-4\right)}\) có giá trị bằng nhau.
NT
0
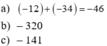
\(\left(y+1\right)+\left(y+4\right)+\left(y+7\right)+...+\left(y+31\right)+\left(y+34\right)=2222\)
\(y+1+y+4+y+7+...+y+31+y+34=2222\)
\(12\times y+\left(34+1\right)\times12:2=2222\)
\(12\times y+210=2222\)
\(12\times y=2222-210\)
\(12\times y=2012\)
\(12\times y=\dfrac{503}{3}\)
\(\left(y+1\right)+\left(y+4\right)+\left(y+7\right)+...+\left(y+31\right)+\left(y+34\right)=222\\ \Leftrightarrow\left(y+y+y+...+y\right)+\left(1+4+7+...+31+34\right)=222\\ \Leftrightarrow12y+210=222\\ \Leftrightarrow12y=222-210=12\\ \Rightarrow y=\dfrac{12}{12}=1\)
* Số các số hạng y là: \(\left(34-1\right):3+1=12\)
* Tổng dãy số từ 1 - 34 là: \(\dfrac{\left(34+1\right).12}{2}\) = 210 ( số )